Schaltnetze und Normalformen

Wie konstruiert man Schaltnetze? Diese Frage wollen wir an dieser Stelle anhand der schon bearbeiteten Aufgabe (Übung Schaltungslogik) klären:

Eine Maschine soll so überwacht werden, dass ein Warnsignal (w = 1) abgegeben wird, wenn eine Störung eintritt (s = 1) und während der Störung der Aufsichtsposten nicht besetzt ist (a = 0) und eine Resettaste nicht gedrückt ist (r = 0). Weiterhin soll das Warnsignal gegeben werden, wenn die Resettaste betätigt ist, obwohl keine Störung vorliegt. Wie sieht das zugehörige Schaltnetz aus?

Eine Analyse der Aufgabe zeigt, dass das Warnsignal W von den drei Variablen S, A und R abhängt. W ist damit eine 3-stellige Schaltfunktion [ W = f(S, A, R) ], deren Funktionstabelle folgendermaßen aussieht:

$\begin{array}{c|c|c||c} s & a & r & w\\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ \end{array}$

Disjunktive Normalform

Die obige Schaltfunktion kann nach folgendem Verfahren aus den drei Grundfunktionen zusammengesetzt werden:

Für alle Kombinationen, für die der Funktionswert W den Zustand 1 hat, werden die vollständigen Konjunktionsterme aufgeschrieben und diese durch ODER-Verknüpfungen zusammengefasst. Ein vollständiger Konjunktionsterm (Vollkonjunktion) ist eine UND-Verknüpfung, die alle Schaltvariablen in negierter oder nicht-negierter Form genau einmal enthält.

Beispiele für Konjunktionsterme

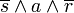• $s \land a \land r$ und $\overline {s} \land a \land \overline {r}$ sind vollständige Konjunktionsterme der Schaltvariablen s, a und r.
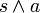• $s \land a$ ist kein vollständiger Konjunktionsterm der Schaltvariablen s, a und r, da r nicht enthalten ist.

Bei n Schaltvariablen gibt es 2ⁿ verschiedene Konjunktionsterme. Da jeder Konjunktionsterm nur bei einer bestimmten Belegung der Schaltvariablen den Wert 1 hat, wird ein Konjunktionsterm auch Minterm genannt.

Den Minterm, der für eine bestimmte Kombination den Wert 1 hat, erhält man, indem man die UND-Verknüpfung aller vorkommenden Schaltvariablen hinschreibt und die Variablen negiert, die bei dieser Kombination den Zustand 0 haben. Demzufolge gilt für unser Beispiel:

Minterm zu Zeile 2: $\overline {s} \land \overline {a} \land r$

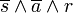
Minterm zu Zeile 4: $\overline {s} \land a \land r$

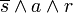
Minterm zu Zeile 5: $s \land \overline {a} \land \overline {r}$

Diese Teilterme (Minterme) werden jetzt mit ODER zusammengefasst. Insgesamt ergibt sich unter Beachtung der Vorrangregeln:

$w = (\overline {s} \land \overline {a} \land r) \lor (\overline {s} \land a \land r) \lor (s \land \overline {a} \land \overline {r})$

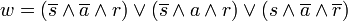
Der damit erhaltene Ausdruck heißt disjunktive Normalform. Die Minterme sind disjunktiv verknüpft.

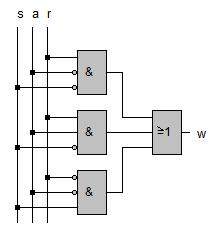
Das Schaltnetz dazu kann man sofort zeichnen.

Konjunktive Normalform

Der Aufbau der obigen Schaltfunktion aus den drei Grundfunktionen ist ebenso nach dem folgenden Verfahren möglich:

Für alle Kombinationen, für die der Funktionswert W den Zustand 0 hat, werden die vollständigen Disjunktionsterme aufgeschrieben und diese durch UND-Verknüpfungen zusammengefasst. Ein vollständiger Disjunktionsterm (Volldisjunktion) ist eine ODER-Verknüpfung, die alle Schaltvariablen in negierter oder nicht-negierter Form genau einmal enthält.

Beispiele für Disjunktionsterme

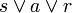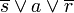• $s \lor a \lor r$ und $\overline {s} \lor a \lor \overline {r}$ sind vollständige Konjunktionsterme der Schaltvariablen s, a und r.

Bei n Schaltvariablen gibt es 2ⁿ verschiedene Disjunktionsterme. Da jeder Disjunktionsterm nur bei einer Kombination der Schaltvariablen den Wert 0 hat, sonst immer den Wert 1 hat, wird ein Disjunktionsterm auch Maxterm genannt.

Den Maxterm, der für eine bestimmte Kombination den Wert 0 hat, erhält man, indem man die ODER-Verknüpfung aller vorkommenden Schaltvariablen hinschreibt und die Variablen negiert, die bei dieser Kombination im Zustand 1 sind. Also gilt:

Maxterm zu Zeile1: $s \lor a \lor r$

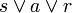
Maxterm zu Zeile3: $s \lor \overline {a} \lor r$

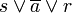
Maxterm zu Zeile6: $\overline {s} \lor a \lor \overline {r}$

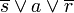
Maxterm zu Zeile7: $\overline {s} \lor \overline {a} \lor r$

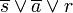
Maxterm zu Zeile8: $\overline {s} \lor \overline {a} \lor \overline {r}$

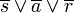
Diese Teilterme (Maxterme) werden jetzt mit UND zusammengefasst. Insgesamt ergibt sich unter Beachtung der Vorrangregeln:

$w = (s \lor a \lor r) \land (s \lor \overline {a} \lor r) \land (\overline {s} \lor a \lor \overline {r}) \land (\overline {s} \lor \overline {a} \lor r) \land (\overline {s} \lor \overline {a} \lor \overline {r})$

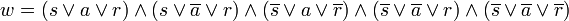
Der so erhaltene Ausdruck heißt konjunktive Normalform. Die Maxterme sind konjunktiv verknüpft.

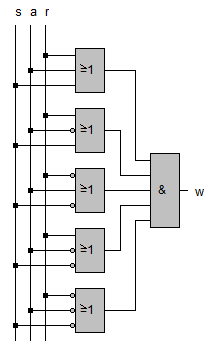
Auch hier lässt sich das zugehörige Schaltnetz sofort zeichnen:

Normalformen und Schaltungssynthese

Zusammenfassend lässt sich sagen, dass jede Schaltfunktion wenigstens in zwei Formen dargestellt werden kann:

Zu jedem booleschen Term gibt es einen äquivalenten Term in disjunktiver Normalform, welcher dadurch entsteht, dass man diejenigen Vollkonjunktionen disjunktiv miteinander verknüpft, für die der Term den Wert 1 hat.

Zu jedem booleschen Term gibt es einen äquivalenten Term in konjunktiver Normalform, welcher dadurch entsteht, dass man diejenigen Volldisjunktionen konjunktiv miteinander verknüpft, für die der Term den Wert 0 hat.

Die Aufstellung einer Wahrheitstabelle und das Ablesen der disjunktiven bzw. der konjunktiven Normalform liefert uns ein allgemein anwendbares Verfahren:

Verfahren zur Schaltungssynthese

1. Aufstellen der Wahrheitstabelle der gesuchten Schaltung.
2. Ablesen einer Normalform: treten als Werte weniger Einsen als Nullen auf, nehme man die disjunktive, andernfalls die konjunktive Normalform.

Mit den oben beschriebenen Verfahren können wir somit zu jeder Schaltfunktion über die Normalformen das zugehörige Schaltnetz entwickeln. Der Nachteil bei dieser Methode ist, dass die Ausdrücke oft sehr groß und redundant werden. Mit Hilfe der Gesetze der Booleschen Algebra bzw. Schaltalgebra lassen sie sich meistens stark vereinfachen. Hierzu braucht man allerdings sehr viel Übung und Einfühlungsvermögen. Es existieren aber auch systematische Vereinfachungsverfahren wie das Quine-McCluskey-Verfahren und das graphische Verfahren von Karnaugh-Veitch (KV-Diagramme).

Das Verfahren der Schaltungssynthese kann also um einen dritten Punkt erweitert werden.

Verfahren zur Schaltungssynthese

1. Aufstellen der Wahrheitstabelle der gesuchten Schaltung.
2. Ablesen einer Normalform: treten als Werte weniger Einsen als Nullen auf, nehme man die disjunktive, andernfalls die konjunktive Normalform.
3. Vereinfachung des booleschen Terms mittels Äquivalenzumformungen

Diese Vereinfachung soll anhand des obigen Beispiels einmal durchgeführt werden. Der boolesche Term für die konjunktive Normalform im vorigen Abschnitt lautete:

$w = (s \lor a \lor r) \land (s \lor \overline {a} \lor r) \land (\overline {s} \lor a \lor \overline {r}) \land (\overline {s} \lor \overline {a} \lor r) \land (\overline {s} \lor \overline {a} \lor \overline {r})$

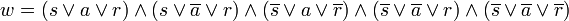
Dieser Term ist sehr komplex und erfordert deshalb ein aufwändigeres Schaltnetz. Mit den Regeln der booleschen Algebra lässt sich der Term folgendermaßen vereinfachen:

$\begin{align} w & = (s \lor a \lor r) \land (s \lor \overline {a} \lor r) \land (\overline {s} \lor a \lor \overline {r}) \land (\overline {s} \lor \overline {a} \lor r) \land (\overline {s} \lor \overline {a} \lor \overline {r}) \\ & = [(s \lor r) \lor (a \land \overline {a})] \land (\overline {s} \lor a \lor \overline {r}) \land [(\overline {s} \lor \overline {a}) \lor (r \land \overline {r})] \\ & = [(s \lor r) \lor 0] \land (\overline {s} \lor a \lor \overline {r}) \land [(\overline {s} \lor \overline {a}) \lor 0] \\ & = (s \lor r) \land (\overline {s} \lor a \lor \overline {r}) \land (\overline {s} \lor \overline {a}) \\ & = (s \lor r) \land [\overline {s} \lor [(a \lor \overline {r}) \land \overline {a})]] \\ & = (s \lor r) \land [\overline {s} \lor [(a \land \overline {a}) \lor (\overline {r} \land \overline {a})]] \\ & = (s \lor r) \land [\overline {s} \lor [0 \lor (\overline {r} \land \overline {a})]] \\ & = (s \lor r) \land [\overline {s} \lor (\overline {r} \land \overline {a})] \end{align}$

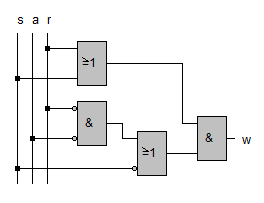
Das zugehörige Schaltnetz nimmt jetzt folgendes Aussehen an: