Boolesche Algebra

George Boole (1815 - 1864) gelang in seinem Buch The Laws of Thought die erste systematische Behandlung der Logik; er entwickelte zu diesem Zweck die algebraische Struktur, die heute als Boolesche Algebra bekannt ist. Die Bedeutung jenes Werkes hat AUGUSTUS DE MORGAN mit folgenden Worten zum Ausdruck gebracht: „Daß die symbolischen Operationen der Algebra, ursprünglich zum Zweck numerischer Rechnungen erfunden, fähig sein sollten, jeden Akt des Denkens auszudrücken sowie Grammatik und Wörterbuch eines umfassenden Systems der Logik zu liefern: dies hätte niemand geglaubt, bevor es in den Laws of Thought bewiesen wurde.“

Allerdings sind die Regeln in ihrer heutigen Form eine Weiterentwicklung durch Mathematiker wie John Venn, W. Stanley Jevons, Charles Peirce, Ernst Schröder und Giuseppe Peano. In Booles originaler Algebra entspricht z. B. die Multiplikation dem UND, die Addition dagegen weder dem exklusiven ENTWEDER-ODER noch dem inklusiven ODER ("mindestens eines von beiden ist wahr"). Die genannten Boole-Nachfolger gingen dagegen vom inklusiven ODER aus.

Die im Folgenden angegebenen Gesetze dienen als Rechenregeln zur Vereinfachung logischer Ausdrücke bzw. boolescher Terme a, b und c. Diese erweiterten Gesetze der Booleschen Algebra, werden auch als Gesetze der Schaltalgebra bezeichnet.

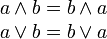$\begin{matrix} a \land b = b \land a \\ a \lor b = b \lor a \end{matrix}$	Kommutativgesetze
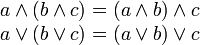$\begin{matrix} a \land (b \land c) = (a \land b) \land c \\ a \lor (b \lor c) = (a \lor b) \lor c \end{matrix}$	Assoziativgesetze
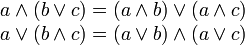$\begin{matrix} a \land (b \lor c) = (a \land b) \lor (a \land c) \\ a \lor (b \land c) = (a \lor b) \land (a \lor c) \end{matrix}$	Distributivgesetze
$\begin{matrix} a \land 1 = a \\ a \lor 0 = a \end{matrix}$	Neutralitätsgesetze
$\begin{matrix} a \land 0 = 0 \\ a \lor 1 = 1 \end{matrix}$	Extremalgesetze
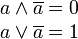$\begin{matrix} a \land \overline {a} = 0 \\ a \lor \overline {a} = 1 \end{matrix}$	Komplementärgesetze
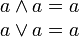$\begin{matrix} a \land a = a \\ a \lor a = a \end{matrix}$	Idempotenzgesetze
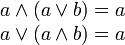$\begin{matrix} a \land (a \lor b) = a \\ a \lor (a \land b) = a \end{matrix}$	Absorptionsgesetze (Verschmelzungsgesetze)
$\begin{matrix} \overline {\overline {a}} = a \end{matrix}$	Doppelnegationsgesetz (Involution)
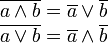$\begin{matrix} \overline {a \land b} = \overline {a} \lor \overline {b} \\ \overline {a \lor b} = \overline {a} \land \overline {b} \end{matrix}$	DE MORGANsche Regeln