Linkslineare Sprachen - reguläre Sprachen
Inhaltsverzeichnis
Definition linkslinearer Sprachen
Es hat sich gezeigt, dass zu viele Fragen offen bleiben, wenn man alle möglichen Regeln ohne Einschränkung zulässt (Allgemeine Regelsprachen). Wir lassen daher nur noch ganz wenige Regeln zu und definieren:
| Definition: Linkslineare Grammatik |
|
Eine Grammatik |
Wir lassen also nur Regeln zu, bei denen ein nichtterminales Zeichen in ein anderes oder sich selbst überführt wird und möglicherweise ein Wort aus terminalen Zeichen folgt, oder bei denen ein nichtterminales Zeichen in ein Wort aus terminalen Zeichen überführt wird. Das Wort aus terminalen Zeichen darf leer sein. Der Name linkslinear kommt daher, dass das nichtterminale Zeichen links steht und dass immer nur ein nichtterminales Zeichen auftritt.
| Definition: Linkslineare Sprache |
|
Eine Sprache heißt linkslinear, wenn es eine linkslineare Grammatik gibt, die diese Sprache erzeugt. |
Schauen wir unsere bisherigen Beispiele an (Einführung - Beispiele oder Beispiele zu allgemeinen Regelsprachen), so scheint es, als wäre die Regeleinschränkung zu stark ausgefallen, denn keine der bisher verwendeten Grammatiken ist linkslinear.
Allerdings haben wir von einer linkslinearen Sprache nur verlangt, dass es eine linkslineare Grammatik zu ihr gibt. Die Sprache zum Beispiel 4 aus Allgemeine Regelsprachen ist eine linkslineare Sprache, denn sie wird auch von folgender linkslinearen Grammatik erzeugt:
G= (VN, VT, P, S) mit
VN = {S}
VT = {0,1}
P = {(S -> S)}
S = S
Im Folgenden soll gezeigt werden, dass es zu den erzeugten Sprachen auch eine linkslineare Grammatik gibt, die diese Sprache erzeugt.
Beispiel 1: Umgangssprachliche Sätze
(siehe Umgangssprachliche Sätze)
Die folgende Grammatik leistet das Gewünschte ... und es ist nicht die einzige mit dieser Eigenschaft.
G = (VN,VT,P,S)
VN = {Nominalphrase,Artikel}
VT = {Susanne,Katze,Pferd,Heu,Buch,der,die,das,jagt,frisst,liest}
P = {(Satz -> Nominalphrase jagt .),
(Satz -> Nominalphrase jagt der Katze .),
(Satz -> Nominalphrase jagt der Pferd .),
(Satz -> Nominalphrase jagt der Heu .),
(Satz -> Nominalphrase jagt der Buch .),
(Satz -> Nominalphrase jagt die Katze .),
...
(Satz -> Nominalphrase frisst .),
...
(Nominalphrase -> Susanne),
(Nominlaphrase -> Artikel Katze),
(Nominlaphrase -> Artikel Pferd),
(Nominlaphrase -> Artikel Heu),
(Nominlaphrase -> Artikel Buch),
(Artikel -> der | die | das)}
S = Satz
Wir mussten lediglich einen Teil der Information, die wir durch Regeln in mehreren Stufen versteckt haben, direkt in die Regeln hineinschreiben. Dadurch ist allerdings die Regelmenge deutlich größer geworden.
Beispiel 2: Bezeichner
Ein Bezeichner in einer pascalähnlichen Sprache soll aus Buchstaben und Ziffern bestehen und mit einem Buchstaben beginnen. Dies wird z. B. durch folgende Grammatik gewährleistet:
G = (VN,VT,P,S)
VN = {Bezeichner,Buchstabe,Ziffer}
VT = {a,...,z,A,...,Z,0,...,9}
P = {(Bezeichner -> Buchstabe | Bezeichner Buchstabe | Bezeichner Ziffer),
(Buchstabe -> a ... z | A ... Z),
(Ziffer -> 0 ... 9)}
S = Bezeichner
Das Beispiel Bezeichner unterscheidet sich vom Beispiel Umgangssprachliche Sätze dadurch, dass die Sprache nicht endlich ist. Die Vorgehensweise zur Umsetzung in eine linkslineare Grammatik ist aber die gleiche.
G = (VN,VT,P,S)
VN = {Bezeichner}
VT = {a,...,z,A,...,Z,0,...,9}
P = {(Bezeichner -> Bezeichner a | ... | Bezeichner z),
(Bezeichner -> Bezeichner A | ... | Bezeichner Z),
(Bezeichner -> Bezeichner 0 | ... | Bezeichner 9),
(Bezeichner -> a ... z | A ... Z)}
S = Bezeichner
Die Beispiele zeigen, dass es durchaus sinnvoll sein kann, eine Sprache durch eine Grammatik eines anderen Typs zu erzeugen.
Eigenschaften linkslinearer Sprachen
- Die leere Menge {} ist linkslinear.
- Wir wählen P = {(S -> S)} für beliebige Mengen VN und VT. Diese zulässige Regel führt nie zu einem terminalen Zeichen. Also ist die zugehörige Sprache leer. (vgl. auch Beispiel 4 aus Allgemeine Regelsprachen).
- Jede einelementige Sprache {w} ist linkslinear.
- Wir wählen P = {(S -> w)}.
- Jede endliche Sprache {w1,w2,...,wn} ist linkslinear.
- Wir wählen P = {(S -> w1 | w2 | ... | wn)}.
- Es gibt unendliche, linkslineare Sprachen.
- Wir wählen als Beispiel
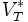 und konstruieren dazu folgende Regelmenge: Zu P sollen dazu genau alle Regeln der Formen (S -> x) und (S -> Sx) für alle
und konstruieren dazu folgende Regelmenge: Zu P sollen dazu genau alle Regeln der Formen (S -> x) und (S -> Sx) für alle 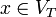 gehören sowie die Regel (S ->
gehören sowie die Regel (S -> 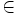 ) zur Erzeugung des leeren Wortes. Hierbei und bei den obigen Begründungen ist
) zur Erzeugung des leeren Wortes. Hierbei und bei den obigen Begründungen ist 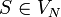 das Startsymbol.
das Startsymbol.
- Sind L1 und L2 linkslineare Sprachen, so ist auch die Vereinigung
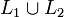 linkslinear.
linkslinear. - Seien L1 = L(G1) mit G1 = (VN1,VT1, P1, S1) und L2 = L(G2) mit G2 = (VN2, VT2, P2, S2) gegeben. Durch eventuelles Umbenennen kann man erreichen, dass VN1 und VT2 disjunkt sind. S sei ein Zeichen, das in ihrer Vereinigung nicht enthalten ist.
Dann erzeugt folgende Grammatik G = (VN, VT, P, S) die gesuchte Sprache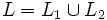 :
:
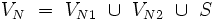
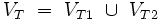


Wenn man aus dem Startzeichen S mit Hilfe der Regel (S, S1) das Startsymbol S1 der Grammatik G1 erzeugt hat, ist es offensichtlich, dass nur noch Worte aus L1 erzeugt werden können und auch genau diese. Entsprechendes gilt für die Worte aus L2.
(Beispiel zur Erläuterung)
- Sind L1 und L2 linkslinear, dann ist auch deren Konkatenation (das Produkt, das durch Anhängen eines Wortes aus L2 an ein Wort aus L1 entsteht) linkslinear.
-

Wir nehmen wieder an, dass VN1 und VN2 disjunkt sind. Sei und
und 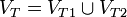 . Das Startzeichen sei S2. In P2 ersetzt man jede Regel der Form (A,w) mit
. Das Startzeichen sei S2. In P2 ersetzt man jede Regel der Form (A,w) mit 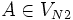 und
und 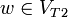 durch (A, S1w). Die neue Regelmenge sei P2’. Mit
durch (A, S1w). Die neue Regelmenge sei P2’. Mit 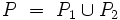 ist man fertig.
ist man fertig.
Durch die besondere Form der Regeln ist gewährleistet, dass jedes aus S2 abgeleitete Wort aus V* maximal ein nichtterminales Zeichen enthält. Dies ist außerdem das erste Zeichen im Wort. Wenn also in G2 eine abschließende Regel angewendet wird, hat man ein Wort aus L2. Genau diese Regel führt in der abgewandelten Grammatik mit P2’ aber das Startzeichen der Grammatik G1 ein. Aus S1 lassen sich noch genau die Worte aus L1 erzeugen, insgesamt also genau die Worte aus L1L2.
Auch hierzu sei ein Beispiel aus der Analyse von Pascal angegeben. Eine vorzeichenlose Realzahl besteht z. B. aus einer vorzeichenlosen Integer Zahl, einem e und einem Exponenten.
- Ist L linkslinear, so ist auch auch
 linkslinear.
linkslinear. - Das Wort wn entsteht dabei, wenn w n-mal hintereinander gehängt wird. Die Beweisidee entspricht der des vorhergehenden Beispiels. In P wird zu jeder abschließenden Regel (A, w) die Regel (A, Sw) hinzugenommen. Falls das leere Wort nicht in L ist, muss es noch durch eine eigene Regel (S,
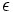 ) erzeugt werden.
) erzeugt werden.
Ein Beispiel aus Pascal ist der Prozedur- und Funktionsdeklarationsteil, denn dieser besteht aus beliebig vielen Prozedur- oder Funktionsdeklarationen, kann aber auch leer sein.
- Ist L linkslinear, so auch das Komplement
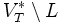 .
. - Der Beweis ist nicht so einfach wie die vorhergehenden. Wir übergehen ihn deshalb.
- Sind L1 und L2 linkslinear, so auch
 .
. - Dies ergibt sich unmittelbar aus den de Morganschen Regeln und den bisher bewiesenen Eigenschaften linkslinearer Sprachen.
Die bisher bewiesenen Eigenschaften linkslinearer Sprachen bilden sehr angenehme Abschlusseigenschaften der Menge der linkslinearen Sprachen. Bei anderen Sprachklassen werden wir davon deutliche Abstriche machen müssen.
Ohne Beweis sei auch angemerkt, dass für linkslineare Grammatiken alle Fragen am Ende des Beitrags Allgemeine Regelsprachen entscheidbar sind.
Beispiele
Für die folgenden Beispiele sei stets das Startzeichen S und VT = {a,b}. Es wird immer P angegeben, und VN enthalte gerade alle dort auftretenden Großbuchstaben.
Beispiel 1
P = {(S -> Sa | Ab),
(A -> a)}
Wir wollen nun feststellen, welche Sprache erzeugt wird. Dazu beginnen wir beim Startzeichen S und versuchen, Regeln anzuwenden. Die Sprache ist so gewählt, dass wir von S ausgehend immer genau zwei Möglichkeiten haben, eine Regel anzuwenden. Von A ausgehend haben wir nur eine Regel. Bei den bisherigen Ableitungen ging es uns immer nur darum, aus dem Startzeichen genau ein vorgegebenes Wort der Sprache zu erhalten. Wenn die Regelmenge einfach ist, kann man auch versuchen, sich einen Überblick über alle Worte der Sprache zu verschaffen, indem man bei jedem Wort alle möglichen Regeln anwendet. Dies könnte dann die Grundidee für einen Beweis liefern. Ein damit zu erstellender Ableitungsbaum könnte so aussehen:
Man erkennt (oder beweist durch Induktion), dass die erzeugte Sprache 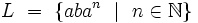 ist.
ist.
Beispiel 2
P = {(S -> Sb | Tb),
(T -> Ta | a)}
Wir erzeugen wieder die Worte der Sprache durch einen Baum:
Man sieht, dass man mit der Regel (S, Sb) Worte der Form Sbm erzeugen kann. Dann kann man das S durch Tb ersetzen und dieses T durch Tan. Zuletzt muss das T durch a ersetzt werden. Alle anderen Möglichkeiten führen nicht zu Worten aus VT*. Damit haben aber alle Worte die Form anbm mit 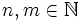 .
.
Beispiel 3 (Grenzen endlicher Automaten)
Wir wollen zu der Sprache  eine Grammatik suchen. Diese Sprache ist uns schon in den Beispielen zu allgemeinen Regelsprachen begegnet. Sie ist für die Syntax von Programmiersprachen von großer Bedeutung, weil sie die einfachste mögliche Klammerstruktur darstellt. Wir denken dabei an arithmetische Ausdrücke mit den Klammern "(" und ")" oder an Verbundanweisungen mit den Klammern BEGIN und END oder an Repeat Anweisungen mit den Klammern REPEAT und UNTIL.
eine Grammatik suchen. Diese Sprache ist uns schon in den Beispielen zu allgemeinen Regelsprachen begegnet. Sie ist für die Syntax von Programmiersprachen von großer Bedeutung, weil sie die einfachste mögliche Klammerstruktur darstellt. Wir denken dabei an arithmetische Ausdrücke mit den Klammern "(" und ")" oder an Verbundanweisungen mit den Klammern BEGIN und END oder an Repeat Anweisungen mit den Klammern REPEAT und UNTIL.
Nach der Art der zugelassenen Regeln (linkslinear oder abschließend) müssen wir aus dem Startzeichen erst die bn erzeugen, dann links davon die an. Dies geht nur mit einem Rekursionsmechanismus. Die einfachste Regel dazu wäre etwa (B, Bb) bzw. (A, Aa). Wir haben dazu nur endlich viele Regeln zur Auswahl, sollen aber beliebig viele b bzw. a erzeugen. Dies geht nur, wenn es gewisse Zyklen der Anwendung von Regeln gibt. Damit kann man dann aber auch zeigen, dass nicht nur Worte mit gleich vielen a's und b's zu einer solchen Sprache gehören. Dies wird in der nebenstehenden Grafik verdeutlicht.
Zu jedem 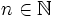 gibt es einen anderen erkennenden Automaten; wir suchen jedoch einen einzigen Automaten, d. h. einen, bei dem die Anzahl der a's nicht beschränkt ist. Dass dies mit einem Automaten, der nur endlich viele Zustände besitzt, nicht geht, leuchtet unmittelbar ein.
gibt es einen anderen erkennenden Automaten; wir suchen jedoch einen einzigen Automaten, d. h. einen, bei dem die Anzahl der a's nicht beschränkt ist. Dass dies mit einem Automaten, der nur endlich viele Zustände besitzt, nicht geht, leuchtet unmittelbar ein.
| Satz: |
|
Wenn die Sprache eines endlichen Automaten Wörter der Form anbn für beliebig große natürliche Zahlen n enthält, dann auch Wörter der Gestalt ambn mit |
Beim Lesen der a's muss der Automat einen Kreis im Zustandsgraphen durchlaufen, wenn er für beliebige Zahlen n anbn erkennen soll. Der Beweis soll an dieser Stelle nicht geführt werden. Diese Sprache ist nicht regulär und kann damit nicht von einem endlichen Automaten erkannt werden.
Zusammenfassung: Nur Sprachen, die keine beliebig tief verschachtelten Strukturen enthalten, können von endlichen Automaten erkannt werden.
- Bereits die Analyse arithmetischer Terme, insbesondere verschachtelter Klammern, übersteigt die Fähigkeiten endlicher Automaten.
- Die Beschränkung der Fähigkeiten endlicher Automaten liegt - ungenau ausgedrückt - daran, dass sie wegen der endlichen Anzahl ihrer Zustände (ihrem "Gedächtnis") nicht beliebig weit zählen können.
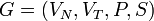 heißt linkslinear, wenn alle Regeln linkslinear, d. h. von der Form (
heißt linkslinear, wenn alle Regeln linkslinear, d. h. von der Form (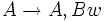 ), oder abschließend, d. h. von der Form (
), oder abschließend, d. h. von der Form (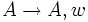 ), sind. Dabei sollen
), sind. Dabei sollen  und
und 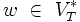 sein.
sein.



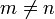 .
.