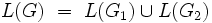Beispiel für Vereinigung linkslinearer Sprachen

Sind L₁ und L₂ linkslineare Sprachen, so ist auch die Vereinigung 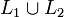$L_1 \cup L_2$ linkslinear. Zur Erläuterung dieser Eigenschaft linkslinearer Sprachen soll ein Beispiel betrachtet werden:

Sei G1 = (VN1, VT1, P1, S1) gegeben mit VN1 = {S,A,B} VT1 = {a,b} P1 = {(S -> Sa | ba)} S1 = S, dann ist $L(G_1)~=~\lbrace ba^n~\mid~n\in \mathbb{N} \rbrace$.	Sei G2 = (VN2, VT2, P2, S2) gegeben mit VN2 = {S,A,B} VT2 = {a,b} P2 = {(S -> Sa | a)} S2 = S, dann ist $L(G_2)~=~\lbrace a^n~\mid~n\in \mathbb{N} \rbrace$.
Es ist $L(G_1) \cup L(G_2)~=~\lbrace b^ma^n~\mid~(m=0 \lor m=1) \land n\in \mathbb{N} \rbrace$.

Um eine Grammatik G für diese Sprache zu finden, benennen wir in G₁ nun S in T um und in G₂ die Zeichen S, A und B in U, V und W. Wir erhalten die neuen Grammatiken G₁’ und G₂’, die die gleiche Struktur wie die alten Grammatiken G₁ und G₂ haben, also auch die gleichen Sprachen erzeugen.

G1’ = (VN1’, VT1’, P1’, S1’) VN1’ = {T,A,B} VT1’ = {a,b} P1’ = {(T -> Ta | ba)} S1’ = T, $L(G'_1)~=~\lbrace ba^n~\mid~n\in \mathbb{N} \rbrace$.	G2’ = (VN2’, VT2’, P2’, S2’) VN2’ = {U,V,W} VT2’ = {a,b} P2’ = {(U -> Ua | a)} S2’ = U, $L(G'_2)~=~\lbrace a^n~\mid~n\in \mathbb{N} \rbrace$.
Daraus ergibt sich sofort die gesuchte Grammatik: G = (VN,VT,P,S) VN = {T,A,B,U,V,W,S} VT = {a,b} P = {(T -> Ta | ba), (U -> Ua | a), (S -> T | U)} S = S $L(G)~=~L(G_1) \cup L(G_2)$

Eine solche Vereinigung taucht bei der Analyse eines Pascalprogramms häufig auf. So ist etwa eine vorzeichenlose Konstante entweder ein Konstantenbezeichner oder eine vorzeichenlose Zahl oder eine Zeichenkette oder das Wortsymbol nil, wobei die ersten drei Begriffe linkslineare Sprachen beschreiben und letzterer eine einelementige. Die obige Regel ist dann mehrfach anzuwenden.

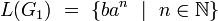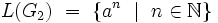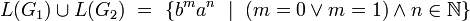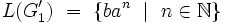(Weitere Eigenschaften linkslinearer Sprachen)