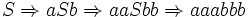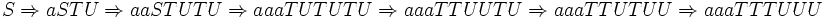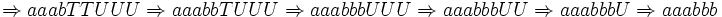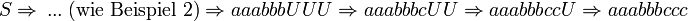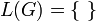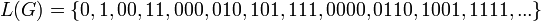Allgemeine Regelsprachen

Allgemeine Regelsprachen entsprechen nach Chomsky Sprachen vom Typ 0. Sprachen dieser Klasse besitzen eine Grammatik, die keiner Einschränkung unterliegen.

Dies wird an einigen Beispielen erläutert.

Beispiel 1

Sei G= (V_N,V_T,P,S) gegeben mit

VN= {S}
VT= {a,b}
P= (S -> ab | aSb)
S= S

Dann ist

$L(G)= \lbrace a^nb^n | n \in N \rbrace$

Als Beispiel sei die Ableitung 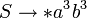$S \rightarrow* a^3b^3$ angegeben:

$S \Rightarrow aSb \Rightarrow aaSbb \Rightarrow aaabbb$

Beispiel 2

Sei G= (V_N,V_T,P,S) gegeben mit

VN = {S,T,U}
VT = {a,b}
P = {(S -> aSTU | aTU),
     (UT -> TU),
     (aT -> ab),
     (bT -> bb),
     (bU -> b)}
S = S

Dann ist

$L(G)= \lbrace a^nb^n | n \in N \rbrace$

Als Beispiel sei die Ableitung 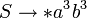$S \rightarrow* a^3b^3$ angegeben:

$S \Rightarrow aSTU \Rightarrow aaSTUTU \Rightarrow aaaTUTUTU \Rightarrow aaaTTUUTU \Rightarrow aaaTTUTUU \Rightarrow aaaTTTUUU$
  $\Rightarrow aaabTTUUU \Rightarrow aaabbTUUU \Rightarrow aaabbbUUU \Rightarrow aaabbbUU \Rightarrow aaabbbU \Rightarrow aaabbb$

Beispiel 3

Sei G= (V_N,V_T,P,S) gegeben mit

VN = {S,T,U}
VT = {a,b,c}
P = {(S -> aSTU | aTU),
     (UT -> TU),
     (aT -> ab),
     (bT -> bb),
     (bU -> bc),
     (cU -> cc)}
S = S

Dann ist

$L(G)= \lbrace a^nb^nc^n | n \in N \rbrace$

Als Beispiel sei die Ableitung 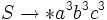$S \rightarrow* a^3b^3c^3$ angegeben:

$S \Rightarrow~...~\mbox{(wie Beispiel 2)} \Rightarrow aaabbbUUU \Rightarrow aaabbbcUU \Rightarrow aaabbbccU \Rightarrow aaabbbccc$

Beispiel 4

Sei G= (V_N,V_T,P,S) gegeben mit

VN = {S,T,U}
VT = {a,b}
P = {(S -> aTU),
     (bU -> a),
     (U -> ST | ab),
     (Tb -> SUb),
     (Ta  -> SaT)}
S = S

Dann ist

$L(G)= \lbrace ~ \rbrace$

Jede Regel, die auf der linken Seite S oder T enthält, enthält auf der rechten ebenfalls S oder T. Jedes Wort, das aus dem Startzeichen S entsteht, enthält also mindestens ein nichtterminales Zeichen.

Beispiel 5

Sei G= (N,T,P,S) gegeben mit

N = {S,T,U}
T = {0,1}
P = {(S -> 0 | 1 | 00 | 11 | 0S0 | 1S1)}
S = S

Dann ist

$L(G)= \lbrace 0, 1, 00, 11, 000, 010, 101, 111, 0000, 0110, 1001, 1111, ... \rbrace$

... die Menge der dualen Palindrome, d. h. derjenigen Dualzahlen, die von vorne und von hinten gelesen das gleiche Aussehen haben. Als Beispiel folgt die Ableitung 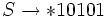$S \rightarrow* 10101$:

$S \Rightarrow 1S1 \Rightarrow 10S01 \Rightarrow 10101$

Fragen zu Grammatiken

Die Beispiele enthalten nur wenige Zeichen, und dennoch kann man bereits erahnen, wie komplex man Grammatiken definieren kann. Es ergeben sich sofort einige wichtige Fragen:

1. Ist die Sprache zu einer Grammatik leer?
2. Ist die Sprache zu einer Grammatik endlich?
3. Gehört ein vorgegebenes Wort zu der von einer vorgegebenen Grammatik erzeugten Sprache?
4. Kann man ein Wort in ein anderes ableiten?
5. Erzeugen zwei Grammatiken dieselbe Sprache (siehe Beispiele 1 und 2)?

Leider sind alle diese Fragen nicht entscheidbar. Den Beweis können wir hier nicht führen und müssen Interessenten auf die Fachliteratur verweisen. Unter nicht entscheidbar verstehen wir intuitiv, dass es kein Verfahren gibt, das uns diese Fragen für beliebige Worte und Grammatiken korrekt beantwortet. Entscheidbarkeit ist sehr eng mit einem präzisen Algorithmusbegriff und mit dem Begriff der Berechenbarkeit gekoppelt.

Letztlich liegt die Ursache der Nichtentscheidbarkeit dieser Fragen darin, dass die Regelmenge ohne jede Struktur sein darf. Dies ist für die Praxis nicht geeignet. Wir wollen uns daher einschränken und nur bestimmte Regeltypen zulassen (z.B. Reguläre Sprachen).