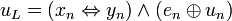Der Subtrahierer

Ebenso wie der Volladdierer entworfen wurde, ließe sich ein Vollsubtrahierer entwickeln, mit dem dann ein Parallelsubtrahierer aufgebaut werden könnte. Dieser Weg wird allerdings nicht weiter beschritten. Stattdessen wollen wir von der bereits erwähnten Tatsache, dass sich alle Rechenarten auf die Addition zurückführen lassen, Gebrauch machen, um ein Subtrahierwerk zu entwickeln. Auf diese Art kommen große Schaltwerke mit einer Rechenschaltung aus, die wahlweise addieren oder subtrahieren kann, was zu erheblichen Einsparungen führt.

Als erstes muss gezeigt werden, wie die Subtraktion - und damit auch die Division als wiederholte Subtraktion - auf eine Addition zurückgeführt werden kann. Den mathematischen Hintergrund zur Subtraktion von Dualzahlen haben wir an anderer Stelle schon erläutert. Diese Überlegungen führen zu folgendem Verfahren der Subtraktion von Zahlen.

Eine Zahl wird subtrahiert, indem man das Zweierkomplement addiert.

Nach diesen Überlegungen zur Durchführung der Subtraktion als Addition des Zweierkomplements des Subtrahenden kann jetzt das zugehörige Schaltnetz für z. B. einen 4-Bit Parallelsubtrahierer entwickelt werden (siehe Aufgaben).

Diese Schaltung hat jedoch noch den Nachteil, dass keine Bereichsüberschreitung (Überlauf) signalisiert wird. Dies ist wichtig, da ein solcher Überlauf unterbunden bzw. zumindest erkannt werden sollte.

Wie die folgenden Beispiele zeigen, können wir hier nicht einfach den Übertrag des letzten Volladdierers benutzen, um eine Bereichsüberschreitung zu erkennen.

Beispiel 1           Beispiel 2           Beispiel 3           Beispiel 4

   -1      1111         -1      1111          1      0001          5       5      0101
+ (-3)   + 1101      + (-8)   + 1000      + (-5)   + 1011      + (+4)  - (-4)   + 0100
------  -------      ------  -------      ------  -------      ------  ------  -------
   -4   (1)1100         -9   (1)0111         -4   (0)1100          9       9   (0)1001

Die Korrektheit der Rechnung kann am Schaltnetz eines 4-Bit-Paralelladdierers überprüft werden.

<flash>file=LogiFlashViewer.swf|width=600|height=450|flashvars=?filestoload=../images/9/93/Ti_4bitadder</flash>

Aus den Beispielen (und evtl. weiteren getesteten Aufgaben) ist zu erkennen, dass der letzte Übertrag nicht ohne weiteres als Überlaufanzeige benutzt werden kann.

Ein Überlauf liegt vor, wenn

1. die höchstwertigen Summandenbits gleich sind und
2. der letzte Übertrag ungleich dem höchstwertigen Ergebnisbit ist.

Bezeichnen wir allgemein die höchstwertigen Bits der Summanden mit x_n und y_n, das höchstwertige Ergebnisbit mit e_n und den letzten Übertrag mit u_n, so lässt sich das Auftreten eines Überlaufs u_L folgendermaßen formal beschreiben:

$u_L = (x_n \Leftrightarrow y_n) \land (e_n \oplus u_n)$

Hierbei steht das Zeichen 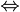$\Leftrightarrow$ für die ÄQUIVALENZ-Funktion und das Zeichen 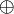$\oplus$ für die XOR-Funktion. Da eine XOR-Funktion relativ häufig eingesetzt werden kann, wird dieses Gatter als Baustein bzw. IC angeboten. Ein ÄQUIVALENZ-Gatter lässt sich durch Negation des Ausganges eines XOR-Gatters realisieren.

Damit sind wir nun in der Lage, den Parallelsubtrahierer so zu erweitern, dass eine Bereichsüberschreitung signalisiert wird. Hierzu müssen die beiden höchstwertigen Summandenbits mit einem ÄQUIVALENZ-Glied und der letzte Übertrag und das höchstwertige Bit des Ergebnisses mit einem EXKLUSIV-ODER-Glied verknüpft werden. Die beiden Verknüpfungsergebnisse werden über ein UND-Glied zum Bereichsüberschreitungssignal zusammengefasst.