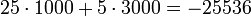Rechnen im Binärsystem
Da dieses Thema ausführlichst an anderen Stellen beschrieben wird, hier nur ein helfender Link:
Subtraktion von Dualzahlen
Jede Subtraktion kann über eine Addition durchgeführt werden.
Beispiel: 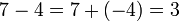
Die Subtraktion der Zahl 4 wird hier durch die Addition der Gegenzahl -4 (inverses Element bezüglich der Addition) ausgeführt. Wir haben damit zwar die Subtraktion umgangen, uns dafür aber das Problem eingehandelt, zu einer Zahl ihre Gegenzahl ermitteln zu müssen. Zu jeder Zahl gibt es bezüglich der Addition eine Gegenzahl, es besteht folgender Zusammenhang:
Zahl + Gegenzahl = 0
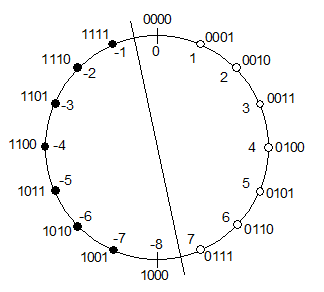
Die Gegenzahlen zu den positiven Zahlen sind die negativen Zahlen. Wir müssen also erst einmal überlegen, wie negative Zahlen im Dualsystem dargestellt werden können. Hierbei spielt die Tatsache, dass jedes Rechenwerk nur mit einer endlichen Anzahl von Stellen zur Darstellung der Zahlen arbeiten kann, eine entscheidende Rolle. Im Computer werden ganze Zahlen als Binärwörter (Bitfolgen) fester Länge dargestellt. Mit der Wortlänge n lassen sich 2n Zahlen binär codieren. Bleibt man im positiven Bereich, so sind das die Zahlen von 0 bis 2n. Zählt man jetzt zur Zahl 2n die Zahl 1 dazu, so gelangt man, da dann das entstandene Übertragsbit das (n+1)-Bit ist und dies nicht mehr zu den n Stellen gehört, zur Zahl 0, codiert durch n Nullen. Die Zahlengerade schließt sich bei Dualzahlen zu einem Zahlenkreis (vgl. Abb.).Geht man auf der Zahlengerade von 0 aus nach links, so gelangt man in den negativen Bereich. Entsprechend müsste man im Zahlenkreis bei Bewegung gegen den Uhrzeigersinn zu den negativen Zahlen kommen und damit 11112 als -1 , 11102 als -2, 11012 als -3 usw. interpretieren.
Wir überprüfen, ob eine solche Interpretation überhaupt möglich ist, indem wir zu einigen Zahlen aus dem rechten Halbkreis die auf gleicher Höhe stehenden Zahlen aus dem linken Halbkreis - die vermutlichen Gegenzahlen - addieren:
1111 0010 0011 + 0001 + 1110 + 1101 ------- ------- ------- (1)0000 (1)0000 (1)0000
In diesen Beispielen ergibt sich als Summe jeweils 0000, da die 1 auf der fünften Stelle wegen der auf vier Stellen beschränkten Zahlendarstellung keine Bedeutung hat. Die Untersuchung weiterer Beispiele führt zum gleichen Ergebnis. An dieser Zahlenkreiseigenschaft ändert sich auch nichts, wenn zur Zahlendarstellung mehr als vier Stellen benutzt werden, hierbei wird lediglich der Zahlenkreis größer.
Eine Sonderrolle spielen die Zahlen 0000 und 1000. Sie sind mit ihren Gegenzahlen identisch. Diese beiden Zahlen markieren die Trennlinie zwischen den positiven und negativen Zahlen. üblicherweise zählt man 10002 = -810 zu den negativen Zahlen und kann damit das Vorzeichen einer Zahl direkt an der ersten Stelle ablesen:
- 1 an erster Stelle heißt negative Zahl
- 0 an erster Stelle heißt positive Zahl
Diese Interpretation der Dualzahlen hat zur Konsequenz, dass bei vierstelliger Darstellung der Zahlenbereich nicht mehr von 0 bis 15 reicht, sondern von -8 bis +7. Der Zahlenbereich umfasst aber nach wie vor 16 Zahlen. Bei 8-stelliger Darstellung reicht der Zahlenbereich demnach von -128 bis +127.
Es bleibt noch zu klären, wie man auf einfache Weise die Gegenzahl zu einer vorgegebenen Zahl ermittelt, ohne dazu einen Zahlenkreis aufzuzeichnen.
- Man bildet das Einerkomplement der Zahl, indem man Stelle für Stelle 1 durch 0 und 0 durch 1 ersetzt.
- Durch Addition von 1 zum Einerkomplement wird das Zweierkomplement gebildet.
Zahl: 0101
Einerkomplement: 1010
+ 1
------
Zweierkomplement: 1011
Die Dualzahl 1011 ist damit das Zweierkomplement zu 0101.
Das Zweierkomplement einer Dualzahl stimmt mit der Gegenzahl bezüglich der Addition überein. Wir erhalten also die Gegenzahl zu einer vorgegebenen Zahl durch Zweierkomplement-Bildung.
| Das Einerkomplement einer Dualzahl erhält man, indem man alle Ziffern invertiert.
Das Zweierkomplement einer Dualzahl wird gebildet, indem man zuerst das Einerkomplement der Zahl bildet und dann eine 1 addiert. |
Bei Verwendung des Zweierkomplements zur Darstellung negativer Zahlen reicht der darstellbare Zahlenbereich bei n Stellen von -2n-1 bis +2n-1-1. Bei der üblichen Darstellung ganzer Zahlen mit 16 Stellen (2 Bytes) ergibt sich somit ein Zahlenbereich von -32768 bis +32767. Aus diesen Überlegungen folgt:
- Wenn man die Zahlenkreiseigenschaft der Zahlendarstellung mit beschränkter Stellenzahl beachtet, sollte es uns nicht mehr wundern, wenn der Computer folgende Rechnung aufmacht
- Das Beispiel macht deutlich, dass ohne Beachtung von Bereichsüberschreitungen bei der Addition zweier positiver Zahlen ein unkorrektes Ergebnis entstehen kann. Um zu korrekten Ergebnisse zu kommen, müssen Zahlbereichsüberschreitungen verhindert werden.