Der Volladdierer

Da bei der Addition mehrstelliger Dualzahlen ein eventueller Übertrag aus vorhergehenden Stellen berücksichtigt werden muss, brauchen wir auch eine Schaltung, die drei einstellige Dualzahlen addieren kann.

Die folgende Tabelle zeigt die benötigte Zuordnung:

$\begin{array}{c c c || c | c} a & b & c & \text {u} & \text {s} \\ \hline 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 1\\ 0 & 1 & 0 & 0 & 1\\ 0 & 1 & 1 & 1 & 0\\ 1 & 0 & 0 & 0 & 1\\ 1 & 0 & 1 & 1 & 0\\ 1 & 1 & 0 & 1 & 0\\ 1 & 1 & 1 & 1 & 1\\ \end{array}$

Die Schaltwerttabelle liefert nach Anwendung der konjunktiven Normalform:

$\begin{align} s & = (a \lor b \lor c) \land (a \lor \overline {b} \lor \overline {c}) \land (\overline {a} \lor b \lor \overline {c}) \land (\overline {a} \lor \overline {b} \lor c) \\ & = (a \lor ((b \lor c) \land (\overline {b} \lor \overline {c})) \land ( \overline {a} \lor ((b \lor \overline {c}) \land (\overline {b} \lor c)) \\ & = (a \lor (b \oplus c)) \land (\overline {a} \lor \overline {b \oplus c})) \\ & = a \oplus (b \oplus c) \end{align}$

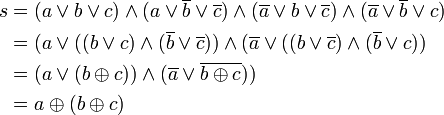
Für den Übertrag liefert die disjunktive Normalform:

$\begin{align} u & = (\overline {a} b c) \lor (a \overline {b} c) \lor (a b \overline {c}) \lor (a b c) \\ & = (((\overline {a} b) \lor (a \overline {b})) c) \lor ((a b) \lor (c \overline {c})) \\ & = (( a \oplus b) c) \lor (a b) \end{align}$

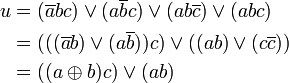
Dieses Ergebnis dürfte auch intuitiv überzeugen: man addiert zunächst a und b, dazu den Übertrag der vorigen Stelle: das ergibt die Summenziffer s. Den Übertrag ü erhält man durch Disjunktion aus den Überträgen a und b der beiden Halbaddierer, da ein gleichzeitiger Übertrag ausgeschlossen ist. Die Schaltung eines Volladdierers kann somit aus Halbaddierern zusammengebaut werden:

Da auch der Volladdierer gibt es einen fertigen Baustein:



Mit den Bausteinen Halbaddierer und Volladdierer lassen sich nun Schaltnetze generieren, die mehrstellige Dualzahlen addieren können (n-Bit Paralleladdierer).