Der Halbaddierer

Zur Entwicklung einer Schaltung, die eine Addition ausführen kann, beginnen wir mit dem einfachsten Fall, der Addition zweier einstelliger Dualzahlen. Nach den Additionsregeln für Dualzahlen ergibt sich folgende Funktionstabelle:

$\begin{array}{c c || c | c} a & b & \text {u} & \text {s} \\ \hline 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 & 0 & 1\\ 1 & 1 & 1 & 0\\ \end{array}$

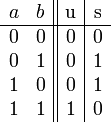
Die Schaltung muss für jede Dualziffer einen Eingang und für die Summe und den Übertrag jeweils einen Ausgang haben. Damit können folgende Schaltfunktionen aufgestellt werden:

$u = a \land b$

$s = (\overline {a} b) \lor (a \overline {b}) = a \oplus b$

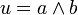
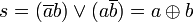
Der Übertrag u wird somit durch eine einfache UND-Schaltung realisiert. Die Summe s durch ein EXCLUSIV-ODER.

Die beiden Teilschaltungen können zu einem Gesamtschaltnetz zusammengefasst werden. Man erhält damit eine Schaltung, die die Addition zweier Dualziffern realisiert. Da diese Schaltung nicht in der Lage ist, einen Übertrag aus einer vorhergehenden Stelle zu verarbeiten, kann sie bei der Addition von Dualzahlen auch nur an der Einerstelle eingesetzt werden. Sie hat daher den Namen Halbaddierer.

Da der Halbaddierer im Folgenden weiter verwendet werden soll - und wir ihn nicht jedesmal mit Hilfe der Grundfunktionen darstellen wollen - verwenden wir in Zukunft einen fertigen Halbaddierer-Baustein:



Um mehrstellige Dualzahlen addieren zu können genügt allerdings kein Halbaddierer, dafür müssen mehrere Halbaddierer zu einem Volladdierer kombiniert werden.