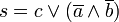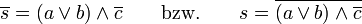Schaltungslogik

Wie werden mit Logikbausteinen Schaltungen entworfen? Dazu ein erstes Beispiel einer Sicherheitsschaltung:

Die Heizölzufuhr für einen Ölofen kann mit zwei Handschaltern (Schalter A im Keller, Schalter B in der Wohnung) ein bzw. ausgeschaltet werden. Ein Sicherheitsschalter C wird durch ein Thermoelement gesteuert, und zwar so, dass C geschlossen wird, wenn die Zündflamme erlischt. In diesem Fall muss die Ölzufuhr unterbrochen und Alarm ausgelöst werden.

Die Schaltung ist so zu konstruieren, dass die Pumpe beim Betätigen von A oder B ein bzw. ausgeschaltet wird. Ist Schalter C geschlossen, soll eine Sperre S aktiviert werden, welche die Pumpe ausschaltet und Alarm auslöst.

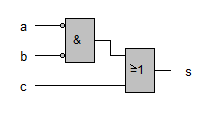
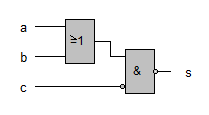
Wir nehmen folgende binäre Darstellung vor: Schalter A geschlossen: a = 1, Schalter B geschlossen: b = 1, Zündflamme erloschen, d. h. Schalter C geschlossen: c = 1, Sperre S aktiviert: s = 1. Dabei entsprechen a, b, c den Eingangssignalen; s ist das Ausgangssignal der Schaltung. Die Bedingung für eine Unterbrechung des Ölzuflusses (Aktivieren der Sperre S) lautet: "Die Zündflamme ist ausgegangen oder keiner der Handschalter ist geschlossen".

Mit den getroffenen Vereinbarungen muss demnach gelten: Die Sperre ist aktiv (s = 1), wenn Schalter A ausgeschaltet ist (a = 0) und Schalter B ausgeschaltet ist (b = 0) oder Schalter C eingeschaltet ist (c = 1). Damit gilt folgende Gleichung: $s = c \lor (\overline {a} \land \overline {b})$ Aus dieser Gleichung lässt sich das nebenstehende Schaltnetz herleiten.
Man kann auch durch folgende Überlegung zu einer Schaltung gelangen: Die Sperre ist inaktiv (Heizöl fließt; s = 0), wenn entweder Schalter A geschlossen (a = 0) oder Schalter B (a = 0) geschlossen ist und die Zündflamme brennt (c = 0); als logischer Ausdruck: $\overline {s} = (a \lor b) \land \overline {c} \qquad \text{bzw.} \qquad s = \overline {(a \lor b) \land \overline {c}}$ Auch aus dieser Gleichung lässt sich ein Schaltnetz herleiten.

Ausdrücke wie die obigen Gleichungen heißen boolesche Terme. Wie können wir uns nun davon überzeugen, dass die beiden Gleichungen auch die gleiche boolesche Funktion darstellen, dass also die zugehörigen Schaltungen genau gleich funktionieren? Nun ja, in unserem Fall können wir das Schaltverhalten mit den gegebenen LogiFlash-Schaltungen überprüfen, aber auf Dauer dürfte dieser Weg zu aufwändig sein.

Eine zweite Möglichkeit, die Gleichungen zu überprüfen, ist eine Wahrheitstabelle (oder: Schaltwerttabelle). Zu diesem Zweck belegen wir die Variablen a, b, c mit Werten aus [0, 1] und vergleichen die Wertverläufe. Damit erhält man für unser Problem die folgenden Wertetabelle:

$\begin{array}{c | c | c || c | c || c | c | c} a & b & c & \overline {a} \land \overline {b} & c \lor (\overline {a} \land \overline {b}) & a \lor b & (a \lor b) \land \overline {c} & \overline {(a \lor b) \land \overline {c}} \\ \hline 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1\\ 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1\\ 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 1 & 0 & 1 & 1 & 0 & 1\\ 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0\\ 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1\\ 1 & 1 & 0 & 0 & 0 & 1 & 1 & 0\\ 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1\\ \end{array}$

Ein Vergleich der fünften mit der achten Spalte zeigt, dass die booleschen Terme wertverlaufsgleich, die zugehörigen Schaltungen also funktionsgleich sind. Wir nennen zwei Terme mit dieser Eigenschaft zueinander äquivalent. Das Erstellen einer Wahrheitstabelle und die Überprüfung boolescher Terme auf Äquivalenz können wir natürlich dem Computer überlassen. Analog zur Zahlenalgebra, in der wir arithmetische Terme umformen, lässt sich die Äquivalenz boolescher Terme durch geeignete Äquivalenzumformungen beweisen. In unserem Fall sieht das so aus:

$\overline {(a \lor b) \land \overline {c}} = \overline {a \lor b} \lor \overline {\overline {c}} = (\overline {a} \land \overline {b}) \lor c = c \lor (\overline {a} \land \overline {b})$

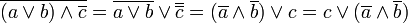
Für diese Äquivalenzumforumungen gelten die Rechenregeln der booleschen Algebra.

Wir wollen uns nun einen Überblick über alle zweistelligen booleschen Funktionen verschaffen. Die beiden Variablen a, b können auf vier verschiedene Arten mit 0 oder 1 belegt werden, daher nimmt eine zweistellige boolesche Funktion f(a,b) genau vier Werte an. Da nun jeder dieser Werte aber 0 oder 1 sein kann, gibt es insgesamt 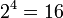$2^4 = 16$ boolesche Funktionen. Wir nennen sie f₀, f₁, ..., f₁₅ und stellen die wichtigsten bei denen beide Argumente eine Rolle spielen in einer Tabelle zusammen:

$\begin{array}{c || c | c | c | c || c | c | c} b= & 0 & 1 & 0 & 1 \\ a= & 0 & 0 & 1 & 1 & \text{Term} & \text{Bezeichnung} & \text{Sprechweise}\\ \hline \hline f_1 & 0 & 0 & 0 & 1 & a \land b & \text{Konjunktion} & a\ \text{AND}\ b\\ f_2 & 1 & 1 & 1 & 0 & \overline {a \land b} & \text{Negatkonjunktion} & a\ \text{NAND}\ b\\ f_3 & 0 & 1 & 1 & 1 & a \lor b & \text{Disjunktion} & a\ \text{OR}\ b\\ f_4 & 1 & 0 & 0 & 0 & \overline {a \lor b} & \text{Negatdisjunktion} & a\ \text{NOR}\ b\\ f_5 & 0 & 1 & 1 & 0 & (\overline {a} \land b) \lor (a \land \overline {b}) & \text{Antivalenz}\ \text{(Exklusiv-Oder)} & a\ \text{XOR}\ b \\ f_6 & 1 & 1 & 0 & 0 & \overline {a} & \text{Erste Negation} & \text{NOT}\ a\\ \end{array}$

Formal schreibt man die Antivalenz mit dem Symbol $\oplus$, es gelten also die Rechenregeln:

$0 \oplus 0 = 0, \quad 0 \oplus 1 = 1, \quad 1 \oplus 0 = 1, \quad 1 \oplus 1 = 0$.

Mit der vollständigen Tabelle aller 16 Funktionen kann man zeigen, dass folgende Sätze gelten:

Alle zweistelligen booleschen Funktionen können mit Hilfe der Negation, der Konjunktion und der Disjunktion dargestellt werden.

Da man aufgrund der Regeln von DE MORGAN die Disjunktion durch Negation und Konjunktion und die Konjunktion durch Negation und Disjunktion ausdrücken können, gilt sogar:

Alle zweistelligen booleschen Funktionen können entweder mit Hilfe der Negation und der Konjunktion oder mit Hilfe der Negation und der Disjunktion dargestellt werden.

Für Funktionen NAND und NOR gilt sogar erstaunlicherweise:

Alle zweistelligen booleschen Funktionen können entweder mit Hilfe der NAND-Verknüpfung oder mit Hilfe der NOR-Verknüpfung dargestellt werden.

Dies hat zur Konsequenz, dass alle Schaltnetze aus Gattern einer einzigen Art aufgebaut werden können. Außerdem sind diese beiden Formen von Gattern technisch am einfachsten realisierbar.

Zusamenfassung

Ein Ausdruck, der aus Variablen und aus den Zeichen für Konjunktion, Negatkonjunktion, Disjunktion, Negatdisjunktion und Negation korrekt gebildet ist, heißt boolescher Term. Jedem boolescher Term entspricht ein binäres Schaltnetz mit einem Ausgang. d. h. eine Schaltung, die aus UND-, ODER-, NICHT-, NAND- und NOR-Gattern korrekt aufgebaut ist. Zwei boolesche Terme sind äquivalent, wenn sie bei jeder Belegung ihrer Eingangsvariablen mit den Werten 0 und 1 den gleichen Wert haben. Äquivalenten booleschen Termen entsprechen funktionsgleiche Schaltnetze.