Binäre Codierung
"... 0110001" schloß Wagstaff zuletzt. "100101" antwortete Ralf Reihe schroff,
"10010111001010101011111100010000100100100000101010101001011010
100101010100010010101010000001111010101011010001001111101010010
10010100100101000000001110100100010010101010000011111100101101"
Die beiden Roboter saßen nebeneinander vor dem großen Steuerpult. Ralf war als Aktenschrank auf zwei
Fahrraupen gebaut, fünf dünne Manipulatoren ragten aus seinem Körper, auf dem ein einziehbarer Sensorkopf
saß. Er hatte kaum sichtbare Leuchten bzw. Anzeigen, und es war schwer zu erkennen, was er dachte.
Abrupt schaltete Ralf Reihe auf Englisch um. Wenn sie sich schon stritten, sollten sie es wenigstens
nicht in den geheiligten Binärzeichen der Maschinensprache tun.
Rudi Rucker: Software
Soll eine Information übermittelt, gespeichert oder verarbeitet werden, muss sie in geeigneter Weise durch Zeichen dargestellt sein. Dieser Vorgang heißt Codierung. Besondere Bedeutung kommt dem Fall zu, dass zur Darstellung genau zwei Zeichen Verwendung finden; dies ist die so genannte binäre Codierung. Diese Idee wirkt bis zur untersten Schicht des Computers hinab.
Die Entdeckung der binären Codierung ist vergleichsweise jungen Datums; am Beginn des automatischen Rechnens stand die - zunächst natürlichere - dezimale Codierung. Als der sechzehnjährige Blaise Pascal im Jahr 1639 sich die Aufgabe stellte, seinen Vater bei dessen mühsamen und zeitaufwendigen Steuerkalkulationen mit einem Rechengerät zu entlasten, musste er zuerst die Frage nach der mechanischen Repräsentation (Darstellung) der Zahlen beantworten. Er fand eine Lösung, die auch heute noch bei Zählern aller Art verwendet wird: jeder Ziffer entspricht die Stellung eines Rades, des Ziffernrades, und das Addieren wird einfach durch Weiterdrehen von Ziffernrädern realisiert (wobei das Problem des Übertrags entsteht).
Rund dreihundert Jahre später steht der Student Konrad Zuse, welcher beschlossen hat, Computererfinder zu werden, vor dem gleichen Problem. In der Zwischenzeit hatte Leibniz die Rechnung mit 0 und 1 (d. h. das System der Dualzahlen) gefunden, wurden von George Boole die mathematischen Gesetze des Denkens aufgestellt (Boolesche Algebra) und ist die Elektrotechnik entstanden. Zuse kommt im Juni 1939 der "entscheidende Gedanke, dass es Elementaroperationen gibt, in die sich sämtliche Rechen- und Denkoperationen auflösen lassen" und die auf der binären Darstellung der Zahlen beruhen. Er erinnert sich:
- "Damals glaubte ich noch, der Vergleich zweier Binärziffern stelle die eigentliche Grundoperation dar. Meine Gedanken faßte ich in einer kleinen Schrift zusammen. Da Leibniz für das binäre Zahlensystem den Ausdruck Dyadik benutzte, nannte ich meine Bedingungskombinatorik "allgemeine Dyadik". In einem Brief an meinen früheren Mathematiklehrer erwähnte ich stolz meine Gedanken. Die Antwort lautete, wie sie lauten mußte: dieser Formalismus sei unter dem Namen Aussagenkalkül längst bekannt."
Bauelemente mit zwei Zuständen funktionieren besonders zuverlässig, Signale mit zwei Werten lassen sich besonders sicher übermitteln. Aber nicht nur dieses technische Argument ist entscheidend, sondern vor allem die Idee, sowohl Rechen- als auch Denkoperationen allgemein auf die binäre Darstellung zu gründen. Rechnen und logisches Schließen haben die gleiche Wurzel. Heute erscheint uns das als mehr oder weniger selbstverständlich. Zu Leibniz’ Zeiten und auch noch zu Beginn dieses Jahrhunderts war es eine umstürzende Erkenntnis, dass sich alle nur denkbaren Daten in binärer Form darstellen und verarbeiten lassen und dass sich hierfür die Elektrotechnik bzw. die Elektronik besonders gut eignen. Dies wurde in der dreißiger Jahren unabhängig voneinander von mehreren Wissenschaftlern, in den Vereinigten Staaten z. B. von Claude Shannon und George Stibitz, erkannt und technisch genutzt.
Wie viele Bits (Binärziffern, engl. binary digit) jeweils notwendig sind, um bestimmte Informationsmengen zu codieren soll an drei Beispielen gezeigt werden:
| Informationsmenge | benötigte Bits | Begründung |
| 10 (Dezimalziffern) | 4 | 10 < 16 = 24 |
| 25 (Buchstaben des Alphabets) | 5 | 25 < 32 = 25 |
| 127 (Anzahl der Zeichen des ASCII) | 7 | 127 < 128 = 27 |
Allgemein können wir feststellen:
Mit Binärwörtern der Länge k lassen sich n Objekte, wobei 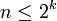 ist, codieren. ist, codieren.
|
Beispiel (Direkter BCD-Code)
Dezimalzahlen werden in elektronischen Rechenanlagen oft nicht unmittelbar in das Dualsystem übersetzt, sondern ziffernweise codiert. Das heißt: Jeder einzelnen Dezimalziffer wird ein vierstelliges Binärwort, eine so genannte Tetrade (von griech.: tetra = vier) zugeordnet. Da es 10 Ziffern, aber 16 Tetraden gibt, werden jeweils 6 Tetraden nicht genutzt; man nennt sie Pseudotetraden. Beim direkten BCD Code (von binär codierte Dezimalziffer) wird jeder Dezimalziffer das Binärwort zugeordnet, welches - als Dualzahl interpretiert - dem Wert der Ziffer entspricht. Also 0 = 0000, 1 = 0001, 2 = 0010, 3 = 0011, ..., 9 = 1001. Dieser Code heißt auch 8421 Code, weil dem Codewort abcd die Zahl 8a + 4b + 2c + d entspricht, das n-te Bit (von rechts) also den Stellenwert 2n besitzt (n = 0, 1, 2, 3).
Zusammenfassung:
| Unter Codierung versteht man die Repräsentation (Darstellung) von Objekten (Gegenständen, Orten, Ereignissen usw.) durch Zeichen. Eine Vorschrift, die angibt, wie die Darstellung durchzuführen ist, heißt Code.
Besteht ein Alphabet (Zeichenvorrat) aus genau zwei Zeichen, so nennen wir die beiden Zeichen Binärzeichen. Eine endliche Folge von Binärzeichen heißt Binärwort, jedes Zeichen eines Binärworts heißt Bit. |
Ein Binärwort der Länge 8, das also aus 8 Bits besteht, heißt Byte. Ein vierstelliges Binärwort wird auch Halbbyte (engl.: nibble) genannt.