Rekursion in Prolog

Definition: Rekursion

Definition eines Problems, eines Verfahrens oder einer Funktion durch sich selbst.

Rekursion ist eines der grundlegenden Arbeitsprinzipien von Prolog. Das Prinzip der Rekursion ist uns schon aus dem Themengebiet OOM bekannt.

Bei einer Rekursion wird das Problem (mit vereinfachten Werten) auf sich selbst zurückgeführt, bis es irgendwann terminiert (Rekursionsende).

Beispiel 1: Vorfahr

In einer früheren Aufgabe war ein Stammbaum von Donald und Daisy gegeben. In den Anfragen wurden u. a. die Eltern und Großeltern gesucht:

% elternteil(Elter,Kind) -- Elter ist Elternteil von Kind
elternteil(Elter,Kind) :-
  vater(Elter,Kind).
elternteil(Elter,Kind) :-
  mutter(Elter,Kind).

% grosselternteil(GElter,Kind) -- GElter ist Großelternteil von Kind
grosselternteil(GElter,Kind) :-
  elternteil(GElter,Elter),
  elternteil(Elter,Kind).

Analog dazu könnte man nun hier auch nach der Urgroßeltern suchen:

% urgrosselternteil(UElter,Kind) -- UElter ist Urgroßelternteil von Kind
grosselternteil(UElter,Kind) :-
  elternteil(UElter,GElter),
  grosselternteil(GElter,Kind).

Es ist natürlich mühsam, für jede weitere Generation von Vorfahren eine weitere Regel aufzustellen, zumal das Bildungsschema klar zu erkennen ist.

Der Begriff Vorfahr wird also teilweise durch sich selbst erklärt. Dies ist ein Kennzeichen der Rekursion, das uns in allen weiteren Beispielen wieder begegnen wird. Damit diese Formulierung nicht unendlich in sich selbst kreist, muss ein Rekursionsende Abbruchkriterium) hinzufügt werden: Ein Elternteil ist ein Vorfahr. Damit sieht die Regel für Vorfahren wie folgt aus:

% vorfahr(X,Y) -- X ist Vorfahr von Y
vorfahr(X,Y) :-
  elternteil(X,Y).
vorfahr(X,Y) :-
  elternteil(X,Z),
  vorfahr(Z,Y).

Die Regel mit dem Rekursionsende sollte immer am Anfang stehen, da es sonst zu Endlosrekursionen kommen kann.

Beispiel 2: Fakultät

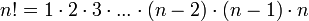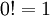Aus der Mathematik (und dem Kurs OOM) ist das Paradebeispiel Berechnung der Fakultät bekannt $n! = 1 \cdot 2 \cdot 3 \cdot ... \cdot (n-2) \cdot (n-1) \cdot n$ mit $0! = 1$. Aus der mathematischen Rekursionsgleichung 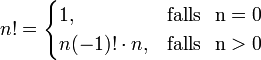$n! = \begin{cases} 1, & \rm{falls ~~ n=0} \\ n(-1)! \cdot n, & \rm{falls ~~ n > 0} \end{cases}$ lassen sich folgende Rekursionsklauseln ableiten:

% fakultaet(N,F) -- F ist Fakultät von N
fakultaet(0,1).
fakultaet(N,F) :-
  N > 0,
  N1 is N - 1,
  fakultaet(N1, F1),
  F is N * F1.

und eine Abfrage liefert:

?- fakulaet(9,Ergebnis).
Ergebnis=362880;

no

Verfolgung einer rekursiven Regel

Die Abarbeitung von Regeln innerhalb von Prolog kann z. B. durch den Trace-Befehl oder auch durch das spur-Prädikat verfolgt werden. An dieser Stelle soll allerdings das write-Prädikat verwendet werden. Die obige Klauseln werden folgendermaßen abgeändert:

% fakultaet(N,F) -- F ist Fakultät von N
fakultaet(0,1) :-
  write('Rekursionsanfang 0! = 1 '), nl.
fakultaet(N,F) :-
  N > 0,
  N1 is N - 1,
  write(' Ich rufe fakultaet('),
  write(N1), write(','), write(F1), write('),'), nl,
  fakultaet(N1,F1),
  F is N * F1,
  write(N), write('! = '),
  write(N1), write('! * '), write(N),
  write(' = '), write(F), nl.

Für einen typischen Aufruf erhalten wir dann:

?- fakultaet(5,Fakultaet).
 Ich rufe fakultaet(4,_L136),
 Ich rufe fakultaet(3,_L148),
 Ich rufe fakultaet(2,_L160),
 Ich rufe fakultaet(1,_L172),
 Ich rufe fakultaet(0,_L184),
Rekursionsanfang 0! = 1 
1! = 0! * 1 = 1
2! = 1! * 2 = 2
3! = 2! * 3 = 6
4! = 3! * 4 = 24
5! = 4! * 5 = 120

Erg = 120 ;

No

Zu sehen ist, wie die Inferenzkomponente bei jedem Rekursionsaufruf für den später noch zu berechnenden Wert einen eigenen Speicherplatz reserviert, z. B. (_L136). Wenn man sich im Detail vorstellen will, wie die Rekursion arbeitet, hilft einem das Schachtelmodell (, welches auch in der OOM Anwendung fand). Jede Schachtel wird dabei von oben betreten, und unten wieder verlassen. Grundsätzlich macht man sich aber tunlichst bei der Formulierung rekursiver Regeln keine Gedanken über diese Feinheiten und überlässt die korrekte Abarbeitung rekursiver Regeln der Inferenzkomponente des Prolog-Interpreters.

Beispiel 3 : Größter gemeinsamer Teiler (ggT)

Wenn man bei kleinen Zahlen den ggT noch relativ rasch erkennt: ggT(49,56) = 7, ist dies bei großen Zahlen nahezu unmöglich. Wie groß ist z. B. der ggT(67474,13097784)? Für den ggT zweier Zahlen existiert die folgende rekursive mathematische Definition: 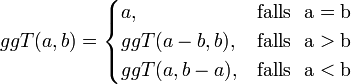$ggT(a,b) = \begin{cases} a, & \rm{falls ~~ a=b} \\ ggT(a-b,b), & \rm{falls ~~ a > b} \\ ggT(a,b-a), & \rm{falls ~~ a < b} \end{cases}$

Zu dieser Definition kann die folgende rekursive Prolog-Regel entwickelt werden:

% ggt(A,B,E) -- E ist das ggT von A und B
ggt(A,A,A).      /* oder umständlicher: ggt(A, A, E) :- E is A. */
ggt(A,B,E) :-
  A > B,
  A1 is A - B,
  ggt(A1,B,E).
ggt(A,B,E) :-
  A < B,
  B1 is B - A,
  ggt(A,B1,E).

... und damit kann die Beispielaufgaben gelöst werden:

?- ggt(67474,13097784, E1), ggt(49,56,E2).
E1=2,
E2=7;

no