Nichtreguläre Sprachen
Wir haben bisher gelernt, dass zu jedem endlichen Akzeptor A mit Eingabealphabet X eine für ihn charakteristische Teilmenge von X* gehört, seine Sprache L(A). Die Umkehrung dieser Tatsache ist jedoch nicht richtig. Es gibt vielmehr Teilmengen von X*, die von keinem Endlichen Automaten erkannt werden können und somit nichtreguläre Sprachen sind. Um dies zu begründen, genügt ein einziges Gegenbeispiel, und wir greifen auf das Beispiel der Achszähleinrichtung zurück.
| Es gibt keinen Endlichen Akzeptor, der genau die Sprache anbn mit n als natürlicher Zahl erkennt. |
Zum Beweis nehmen wir an, dass es einen solchen Automaten mit dem Eingabealphabet X={a,b} und m Zuständen gibt, der genau die Worte der Sprache 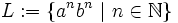 erkennt. Wir zeigen dann, dass im Widerspruch zu dieser Annahme der Automat zusätzlich Worte erkennt, die nicht zu L gehören, dass also
erkennt. Wir zeigen dann, dass im Widerspruch zu dieser Annahme der Automat zusätzlich Worte erkennt, die nicht zu L gehören, dass also 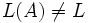 , nämlich
, nämlich 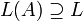 , ist.
, ist.
Der Automat hat endlich viele Zustände. Wir wählen nun ein spezielles Wort aMbM der Sprache L, das genügend viele a enthält, nämlich mehr als die Zustandszahl m. Wir wählen also M > m. Beim Abarbeiten des Teilworts aM kann der Automat nicht M verschiedene Zustände durchlaufen, denn er hat ja nur m, und es ist m < M. Es wird also mindestens ein Zustand z zweimal durchlaufen. Beim Abarbeiten des Worts aMbM durchläuft der Automat also wenigstens einmal einen Zyklus vom Zustand z in den Zustand z und gelangt schließlich in einen Endzustand, da das Wort zu seiner Sprache gehört. Dieser Zyklus kann nun auch bei entsprechend höherer Anzahl N der a mehrfach durchlaufen werden oder bei entsprechend niedriger überhaupt nicht, und der Automat gelangt auch beim Abarbeiten des Worts aNbM mit 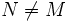 in denselben Endzustand. Also akzeptiert der Automat eine L umfassende Wortmenge.
in denselben Endzustand. Also akzeptiert der Automat eine L umfassende Wortmenge.
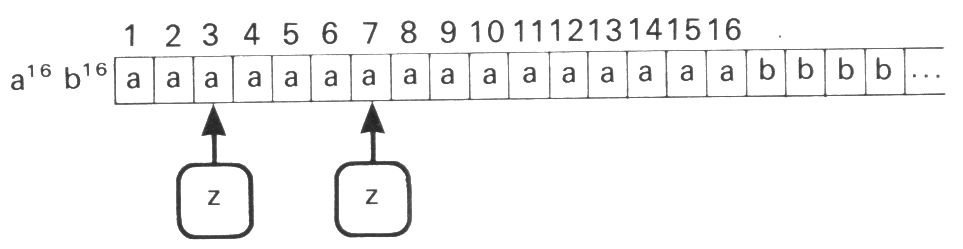
Die grundlegende Beweisidee veranschaulichen wir an folgendem Beispiel mit M=16 und N=12.
Hier haben wir ohne Beschränkung der Allgemeinheit angenommen, dass der Automat beim dritten und siebten a im Zustand z ist.
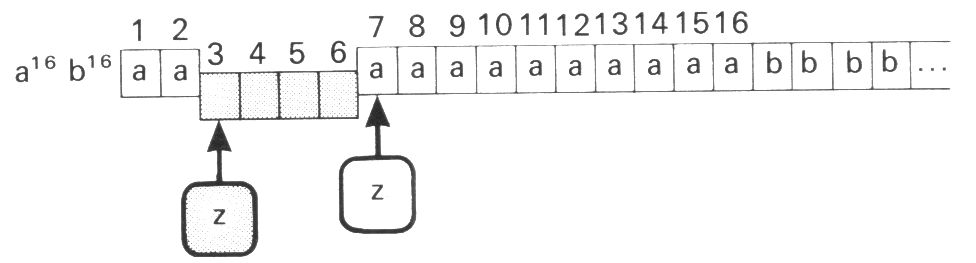
Schneiden wir das Teilwort aaaA heraus oder kopieren es nochmals in das Wort hinein, arbeitet der Automat wie vorher weiter.
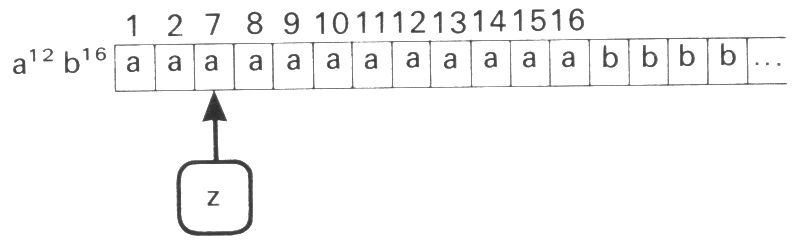
Der Automat gelangt daher auch nach Abarbeitung von a12b16 in denselben Endzustand wie bei a16b16. Er akzeptiert also a12b16, was nicht in L enthalten ist. Entsprechend akzeptiert er auch a20b16, a24b16, a28b16, ... Widerspruch.
Wir haben damit nachgewiesen, dass das Modell des Endlichen Automaten in seiner Leistungsfähigkeit begrenzt ist; es reicht nicht aus, um beliebige Wortmengen zu beschreiben. Ein Endlicher Automat kann sich nur in seinen endlich vielen Zuständen etwas "merken", er "weiß" nur das zuletzt Gelesene und ist sehr "vergesslich".
Eine Folge unseres obigen Satzes ist, dass kein Endlicher Automat beliebig tief geschachtelte Klammerstrukturen in algebraischen Ausdrücken oder beliebig tief geschachtelte BEGIN ... END Strukturen in Pascal erkennen kann. Für die Syntaxanalyse von Pascalprogrammen ist daher dieses Automatenmodell nicht ausreichend.