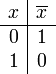Grundfunktionen
Inhaltsverzeichnis
Die folgende Tatsache ist für den Aufbau logischer Schaltung und besonderer Bedeutung.
| Jede Schaltfunktion lässt sich auf die drei Grundfunktionen AND, OR und NOT zurückführen. Diese Grundfunktionen – häufig auch Grundverknüpfungen genannt - bilden damit ein vollständiges System und sind selbst nicht weiter "zerlegbar" |
In der Schaltalgebra heißt eine Menge von Verknüpfungen vollständig, wenn sich jede Schaltfunktion allein mit Hilfe von Verknüpfungen dieser Menge darstellen lässt
Konjunktion
| Definition: Konjunktion |
|
Als Konjunktion (AND-Verknüpfung, UND-Verknüpfung) wird eine boolesche Funktion bezeichnet, die das folgende Funktionsverhalten besitzt:
|
Eine Konjunktion wird durch das Verknüpfungszeichen 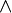 gekennzeichnet. Neben der Darstellung
gekennzeichnet. Neben der Darstellung 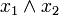 (lies: "x1 und x2") sind allerdings auch
(lies: "x1 und x2") sind allerdings auch 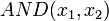 ,
, 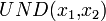 und
und 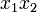 möglich.
möglich.
Eine elektronische Schaltung zur Realisierung der Konjunktion wird UND-Schaltung, UND-Glied oder auch AND-Gatter genannt.
Eine Konjunktion besitzt mindestens zwei Eingänge, da aber auch mehr Eingänge zulässig sind, gilt allgemein:
| Der Ausgang einer UND-Schaltung hat nur dann den Zustand 1, wenn alle Eingänge den Zustand 1 haben. In allen anderen Fällen hat der Ausgang den Zustand 0. |
Disjunktion
| Definition: Disjunktion |
|
Als Disjunktion (OR-Verknüpfung, ODER-Verknüpfung) wird eine boolesche Funktion bezeichnet, die das folgende Funktionsverhalten besitzt:
|
Eine Disjunktion wird durch das Verknüpfungszeichen 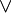 gekennzeichnet. Neben der Darstellung
gekennzeichnet. Neben der Darstellung 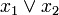 (lies: "x1 oder x2") sind allerdings auch
(lies: "x1 oder x2") sind allerdings auch 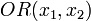 und
und 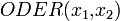 möglich.
möglich.
Eine elektronische Schaltung zur Realisierung der Disjunktion wird ODER-Schaltung, ODER-Glied oder auch OR-Gatter genannt.
Eine Disjunktion besitzt mindestens zwei Eingänge, da aber auch mehr Eingänge zulässig sind, gilt allgemein:
| Der Ausgang einer ODER-Schaltung hat den Zustand 1, wenn wenigstens ein Eingang den Zustand 1 hat. |
... oder anders ausgedrückt ...
| Der Ausgang einer ODER-Schaltung hat nur dann den Zustand 0, wenn alle Eingänge den Zustand 0 haben. |
Negation
| Definition: Negation |
|
Als Negation (NOT-Verknüpfung, NICHT-Verknüpfung) wird eine einstellige boolesche Funktion bezeichnet, die das folgende Funktionsverhalten besitzt:
|
Eine Negation wird durch das Verknüpfungszeichen 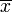 (Überstrich) gekennzeichnet. Neben der Darstellung
(Überstrich) gekennzeichnet. Neben der Darstellung 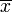 (lies: "nicht x") sind allerdings auch
(lies: "nicht x") sind allerdings auch  ,
, 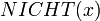 und
und 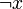 möglich.
möglich.
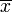 kann auch als Negat oder Komplement bezeichnet werden.
kann auch als Negat oder Komplement bezeichnet werden.
Eine elektronische Schaltung zur Realisierung der Negation wird NICHT-Schaltung, NICHT-Glied, NOT-Gatter, Negator oder auch Inverter genannt.
| Der Ausgang einer NICHT-Schaltung hat stets den Zustand, den der Eingang nicht hat. |
Zusammenfassung
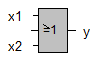
| Grundfunktion | Schaltsymbol (DIN 40700) | schaltalgebraische Darstellung | Funktionstabelle | Testschaltung |
| Konjunktion (AND) |
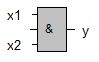 |
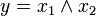 |
 |
|
| Disjunktion (OR) |
 |
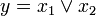 |
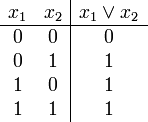 |
|
| Negation (NOT) |
 |
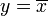 |
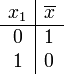 |
Bei einer Zusammenschaltung von NICHT-Gliedern mit UND-Gliedern bzw. ODER-Gliedern braucht die NICHT-Verknüpfung nicht gesondert dargestellt zu werden. Stattdessen kann man die Negation am jeweiligen Eingang oder Ausgang durch einen kleinen Kreis (Negationspunkt) kenntlich machen.
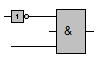 |
kann abgekürzt werden durch | 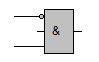
|
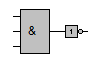 |
kann abgekürzt werden durch | 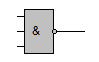
|
Um bei der schaltalgebraischen Beschreibung von Schaltfunktionen Klammern sparen zu können, werden folgende Vorrangregeln vereinbart:
| NICHT hat Vorrang vor UND; UND hat Vorrang vor ODER. |