Endlichen Automaten als binäres Schaltwerk
Inhaltsverzeichnis
Hardware and software are logically equivalent.
One person’s hardware is another person’s software.
Tannenbaum
An dieser Stelle soll die Realisierung endlicher Automaten durch Schaltnetze und Speicherelemente diskutiert werden; dies führt zum Begriff des binären Schaltwerks.
Aus der Definition des endlichen Automaten ergibt sich, dass ein binäres Schaltwerk folgende Bestandteile enthalten muss:
- Erstens ein Schaltnetz, das aus aktuellem Zustand und Eingabe den jeweiligen Folgezustand ermittelt (Realisierung der Übergangsfunktion des Automaten),
- Zweitens ein Schaltnetz, das die Ausgabe bereitstellt (Realisierung der Ausgabefunktion des Automaten),
- Drittens einen Speicher, der dafür sorgt, dass der Momentanzustand bis zum nächsten Taktimpuls erhalten bleibt; für ihn wird man das Universal Speicherelement (JK-Flipflop) verwenden.
Beispiel Warenautomat
Aufgabenstellung
Ein Warenautomat liefert gegen Einwurf eines 2€-Stücks oder zweier 1€-Stücke eine Ware. Nach Drücken des Rückgabeknopfs gibt er bereits eingeworfenes Geld zurück, sofern 2 € noch nicht erreicht sind; andernfalls befördert er die Ware ins Entnahmefach.
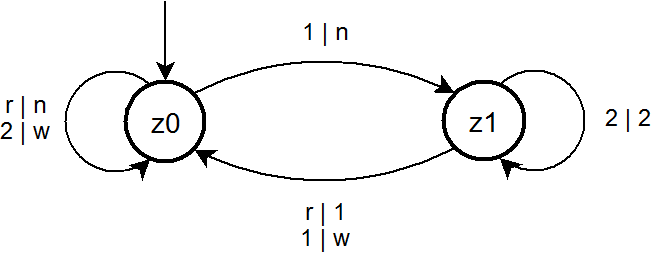
Zustandsgraph des Automaten
Das Eingabealphabet des Automaten sei  , wobei "r" das Drücken des Rückgabeknopfs bedeutet. Das Ausgabealphabet sei
, wobei "r" das Drücken des Rückgabeknopfs bedeutet. Das Ausgabealphabet sei  wobei "w" für Ware, "n" für Nichts und "1" bzw. "2" für Rückgabe eines der Eurostücks steht (die Rückgabe des 2€-Stücks ist nicht möglich). Die Zustandsmenge ist
wobei "w" für Ware, "n" für Nichts und "1" bzw. "2" für Rückgabe eines der Eurostücks steht (die Rückgabe des 2€-Stücks ist nicht möglich). Die Zustandsmenge ist 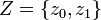 , wobei
, wobei 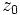 der neutrale Anfangs- (und zugleich Endzustand) ist. Den Zustandsgraphen zeigt die folgende Abbildung.
der neutrale Anfangs- (und zugleich Endzustand) ist. Den Zustandsgraphen zeigt die folgende Abbildung.
Aufstellen der Schaltfunktion
Zunächst müssen Eingabezeichen, Ausgabezeichen und Zustände als Binärwörter dargestellt werden. Wir nehmen folgende (subjektive) binäre Codierung vor:
| Eingabezeichen | Ausgabezeichen | Zustände | |||
| 01 | 1 € eingeworfen | 00 | nichts | 0 | z0 |
| 10 | 2 € eingeworfen | 01 | 1 € zurückgegeben | 1 | z1 |
| 11 | Resettaste gedrückt | 10 | 2 € zurückgegeben | ||
| 11 | Ware ausgeben | ||||
Aus dem Zustandsgraphen leitet sich folgende Schaltwerttabelle her:

Zu beachten ist hier, dass die Eingaben  und
und 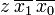 praktisch nicht definiert sind - in diesem Fall müssen die aktuellen Zustände für
praktisch nicht definiert sind - in diesem Fall müssen die aktuellen Zustände für 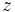 ,
,  und
und 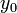 erhalten bleiben.
erhalten bleiben.
Damit lassen sich folgende boolesche Funktionen aufstellen:
Übergangsfunktion: 
Ausgabefunktion: 
Konstruktion des Schaltnetzes
Die Übergangs- und die Ausgabefunktion können durch je ein Schaltnetz realisiert werden. Das der Übergangsfunktion entsprechende Schaltnetz heißt auch Übergangsschaltnetz (engl.: next state logic); das der Ausgabefunktion entsprechende Schaltnetz heißt Ausgabeschaltnetz (engl.: output logic). Ferner benötigt man ein Verzögerungselement, das in der Lage ist, 1 Bit zu speichern, nämlich den aktuellen Zustand. Denn der von der Übergangsfunktion erzeugte Folgezustand muss eine Taktperiode lang gespeichert werden, um in der nächsten Periode an Übergangs- und Ausgabeschaltnetz anzuliegen.
Das im Flash dargestellte binäre Schaltwerk arbeitet wie folgt: Zu einem beliebig herausgegriffenen Zeitpunkt t liegen die Eingangsgrößen x = (x0, xl) an, und das Schaltwerk befindet sich im Zustand z. Aus x und z bildet das Übergangsschaltnetz den Folgezustand zf, der am Eingang des Speicherelements zur Übernahme bereitsteht. Das Ausgabeschaltnetz erzeugt aus x und z die Ausgangsgröße y = (y0, yl). Zum nächsten Zeitpunkt t' wird dann der Folgezustand zf in den Speicher übernommen und dadurch zum neuen internen Zustand z. Aus z und der nunmehr anliegenden Eingangsgröße x bildet das Schaltnetz f den neuen Folgezustand zf usw. Die Zeitpunkte t, t', t", ... werden durch ein dem Speicherelement zugeführtes Taktsignal festgelegt, das jeweils die Übernahme des Folgezustands auslöst. Das Speicherelement arbeitet wie eine Art Schleuse, indem es den an seinem Eingang liegenden Zustand beim nächsten Taktimpuls an seinen Ausgang weitergibt. Charakteristisch für Schaltwerke ist offenbar die Rückkopplung, d. h. die Rückführung der Leitung, welche den aktuellen Zustand transportiert, zum Eingang des Übergangsschaltnetzes.