Begriffsbestimmungen

In diesem Beitrag werden wir die elementaren Bausteine kennen lernen, aus denen informationsverarbeitende Geräte bestehen: die digitallogischen Gatter. In dem Wort digitallogisch klingen zwei geistige Wurzeln der Informationstechnik an: der Bestandteil logisch bezieht sich auf die Aussagenlogik als das Rechnen mit Wahrheitswerten; der Wortbestandteil digital verweist auf das Rechnen mit Zahlen (wofür bekanntlich auch die Finger dienen können). Digitus (lat.) = Finger bezeichnet die Eigenschaft, nur diskrete Werte annehmen zu können. Beim Zählen mit den Fingern gibt es keine Zwischenwerte. Im Gegensatz dazu bezeichnet analog die Eigenschaft, Zwischenwerte annehmen zu können.

Auf Gottfried Wilhelm Leibniz geht die Idee zurück, das Rechnen mit Zahlen, allgemein: jedes gedankliche Operieren mit Zeichen, auf das Rechnen mit Null und Eins zurückzuführen. Er sagt:

Aber das Binärsystem, das heißt, das Rechnen mit 0 und 1, ist trotz seiner Länge das grundlegendste System für die Wissenschaft und führt zu neuen Entdeckungen, die dann für den Umgang mit Zahlen nützlich sind. Wenn die Zahlen auf ihre einfachsten Prinzipien wie 0 und 1 reduziert werden, herrscht überall eine wunderbare Ordnung.

An dieser Stelle sehen wir davon ab, dass Informationsverarbeitung - als Vorgang der realen Welt - Zeit benötigt. Das heißt, wir treffen die idealisierende Annahme, dass das Ergebnis sofort zur Verfügung steht. Geräte, die auf diese Weise arbeiten, heißen Zuordner; man kann sie auch als Systeme ohne Gedächtnis auffassen. Technisch lassen sich Zuordner durch binäre Schaltnetze realisieren, d. h. durch das Zusammenschalten digitallogischer Gatter. Stellt man ein Schaltnetz zeichnerisch dar, erhält man einen gerichteten Graphen ohne Zyklen.

Der englische Mathematiker George Boole (1815 – 1864) entwickelte in seinem Buch "The Laws of Thought" zur systematischen Behandlung der Logik eine algebraische Struktur, die heute als Boolesche Algebra bekannt ist. Die Schaltalgebra ist eine wichtige Anwendung der Booleschen Algebra im technischen Bereich und dient zur Beschreibung und Untersuchung logischer Schaltungen und somit zur Entwicklung automatischer Steuerungen und elektronischer Rechenanlagen.

Eine Schaltvariable ist eine Veränderliche, die nur eine bestimmte Anzahl verschiedener Zustände annehmen kann. Sie wird deshalb auch als digitale Veränderliche bezeichnet. In der Technik werden meistens zweiwertige (binäre) Schaltvariable verwendet. Diese Variable können nur zwei Zustände, die so genannten Binärzustände, annehmen, die mit den Symbolen 0 und 1 gekennzeichnet werden.

In logischen Schaltungen werden fast ausschließlich Spannungswerte als Variable verwendet. Man definiert entweder niedrige Spannung als 0 und hohe Spannung als 1 (positive Logik) oder hohe Spannung als 0 und niedrige Spannung als 1 (negative Logik). In der TTL Technik (TTL = Transistor-Transistor-Logik) werden den Binärzuständen 0 und 1 nach Ein- und Ausgang verschieden folgende Spannungspegel zuordnet:

Eingang:    0 := 0 – 0,8 V;   1 := 2,0 – 5 V
Ausgang:    0 := 0 – 0,4 V;   1 := 2,4 – 5 V

Auch Schalter in einem Stromkreis stellen zweiwertige Schaltvariable dar. Sie können offen (=0) oder geschlossen (=1) sein.

Eine n-stellige Schaltfunktion f ordnet jedem n-Tupel von Schaltzuständen aus $D \subset \lbrace 0,1\rbrace^n, n \in \N$, eindeutig einen der beiden Schaltzustände 0 oder 1 zu. Schreibweise:

$f: D \rightarrow \lbrace 0,1 \rbrace; \qquad (a_1, a_2, ..., a_n) \rightarrow f(a_1, a_2, ..., a_n)$

Prinzip einer Logikschaltung

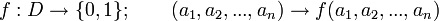
Eine elektronische Schaltung, die eine Schaltfunktion realisiert, heißt logische Schaltung.

Die unabhängigen Variablen 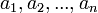$a_1, a_2, ..., a_n$ nennt man Eingangsvariable oder kurz Eingänge, das Funktionsergebnis 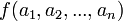$f(a_1, a_2, ..., a_n)$ Ausgangsvariable oder kurz Ausgang.

Die an den Eingängen vorliegenden Schaltzustände werden Eingangssignale, der Schaltzustand des Ausganges wird Ausgangssignal genannt.

Eine Schaltfunktion f wird meist in Form einer Funktionstabelle angegeben und häufig als Verknüpfung der Schaltvariablen bezeichnet.

---

Beispiel

a und b seien Schaltvariable und f eine 2-stellige Schaltfunktion, die durch folgende Tabelle definiert ist

$\begin{array}{c c | c} a & b & f(a{,}b)\\ \hline 0 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 1\\ 1 & 1 & 1\\ \end{array}$

---

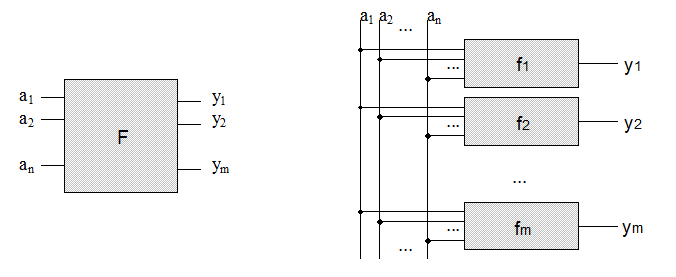
Schaltungen mit mehreren Ausgängen lassen sich aus einzelnen Schaltungen mit je einem Ausgang zusammensetzen, wie die folgende Abbildung verdeutlicht.

F stellt hier ein Funktionsbündel dar:

$F(a_1, a_2, ..., a_n) = (y_1, y_2, ..., y_m) \qquad \text{mit} \qquad \begin{matrix} y_1 = f_1(a_1, a_2, ..., a_n) \\ y_2 = f_2(a_1, a_2, ..., a_n) \\ ... \\ y_m = f_m(a_1, a_2, ..., a_n) \end{matrix}$

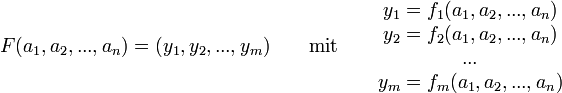
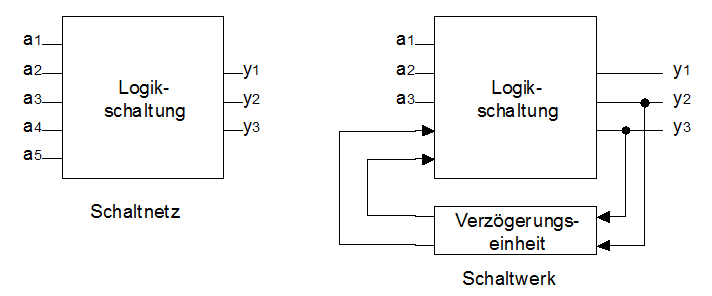
Definition: Schaltnetz & Schaltwerk

Eine Logikschaltung heißt Schaltnetz, wenn der Zustand des Ausganges zu jedem Zeitpunkt nur von den Schaltzuständen der Eingänge abhängt. Hängt der Ausgangszustand jedoch noch von früheren Eingangszuständen ab – dies ist durch ein Rückkopplung eines oder mehrer Ausgänge über eine Verzögerungseinheit auf einen oder mehrere Eingänge möglich – so handelt es sich um ein Schaltung "mit Gedächtnis" und wird Schaltwerk genannt.