Übungsaufgaben Rekursion in Prolog

Aufgabe 1

In der Mathematik gibt es eine Menge von Zahlenreihen, die durch genau definierte mathematische Bildungsgesetze generiert werden, z. B. die Fibonacci-Zahlen. Sie werden rekursiv gebildet, indem man jeweils die letzte und die vorletzte Fibonacci-Zahl addiert:

$fib(n) = \begin{cases} 0, & \rm{falls ~~ n=0} \\ 1, & \rm{falls ~~ n=1} \\ fib(n-1)+fib(n-2), & \rm{falls ~~ n>1} \end{cases}$

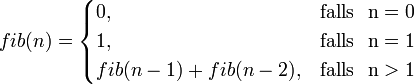
Implementiere in Prolog ein Prädikat fib(N,E), welches in E die Fibonacci-Zahl von N berechnet. Es müsste die Zahlenfolge 0 – 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – … entstehen. Berechne auch den Wert für fib(25), fib(35), fib(50) und fib(100).

---

Aufgabe 2

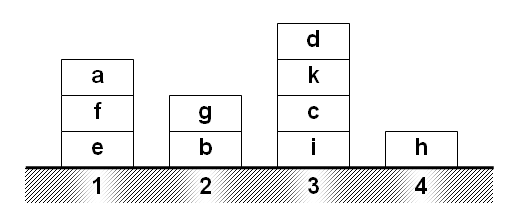
Auf den Plätzen 1 bis 4 liegen die Blöcke a bis k in der dargestellten Anordnung:

Die Anordnung lässt sich folgendermaßen in einer Datenbasis erfassen:

% liegt_auf(X,Y) -- X liegt auf Y
liegt_auf(e,1).
liegt_auf(f,e).
...

1. Programmieren Sie eine Regel ist_platz(X), welches Plätze erkennt:

?- ist_platz(1).
true.

?- ist_platz(e).
false.

2. Es soll eine rekursive Regel ueber(X,Z) definiert werden, mit der Bedeutung, dass X (irgendwo) über Z liegt. Diese Regel soll z. B. das folgende Ergebnis liefern:

?- ueber(a,f).
true.

?- ueber(Was,c).
Was = k;
Was = d;
false.

?- ueber(g,Wen).
Wen = b;
Wen = 2;
false.

---

Aufgabe 3

Paul ist von der rekursiv definierten Fakultätsfunktion total begeistert.

1. Leider hat er deren Definition vergessen. Wie lautet die genaue, eindeutige Definition der Fakultätsfunktion? Berechnen Sie 5!.
2. Paul hat sich in seiner Freizeit eine eigene rekursive Funktion ausgedacht, die er paulitaet nennt. Es gilt:
   $paulitaet(n) = \begin{cases} 2, & \rm{falls ~~ n=0} \\ (n+1) \cdot paulitaet(n-1), & \rm{falls ~~ n>0} \end{cases}$
   Berechnen Sie paulitaet(4) ausführlich.
3. Entwerfen Sie eine zweistellige rekursive Prolog-Regel, welche die gewünschten Ergebnisse liefert.

---

Aufgabe 4

Auf der Weltausstellung 1899 zu Paris hatte der Mathematiker Edouard Lucas etliche seiner mathematischen Spiele ausgestellt – darunter das Spiel Türme von Hanoi. Mehrere kreisförmige Scheiben sind der Größe nach auf einem der drei Stifte gestapelt. Ziel des Spiels ist es, den Turm auf einen anderen der beiden Plätze umzubauen. Dabei müssen die Scheiben einzeln von einem Stapel auf einen anderen umgelegt werden, ohne dass je eine größere Scheibe über eine kleinere zu liegen kommt.

Definieren Sie ein Prädikat umgestapelt(N,A,B,C) mit der Bedeutung "der Turm von N Scheiben wird von Platz A nach Platz B unter Benutzung des Hilfsplatzes C umgestapelt". Die Aufgabe des Umstapelns wird rekursiv gelöst, indem wir das Umstapeln eines Turms von N Scheiben auf das eines Turmes von N - 1 Scheiben und das Umlegen einer einzelnen Scheibe zurückführen:

• Der Turm der oberen N - 1 Scheiben wird von A nach C (unter Benutzung von B) umgestapelt.
• Die verbliebene unterste Scheibe wird von A nach B umgelegt.
• Der Turm von N - 1 Scheiben wird von C nach B (unter Benutzung von A) umgestapelt.
• Der Vorgang ist beendet, wenn N = 0 geworden ist (Rekursionsanfang).

Das Prolog-Programm könnte z. B. die folgende Lösung liefern:

?- hanoi(3).
Die oberste Scheibe wird jeweils wie folgt umgelegt :
a nach b
a nach c
b nach c
a nach b
c nach a
c nach b
a nach b
yes

Ein Teil des Programms könnte dieses Aussehen haben:

hanoi(N):-
  write(’Die oberste Scheibe wird jeweils wie folgt umgelegt : ’), nl, nl,
  umgestapelt(N, a, b, c).

Entwerfen Sie eine vierstellige rekursive Prolog-Regel umgestapelt(N,A,B,C), welche die Türme umstapelt und dies in der obigen Art dokumentiert.