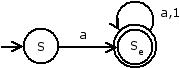
Äquivalenz links- bzw. rechtslinearer Sprachen und endlicher Automaten

Es gilt:
Zu jeder linksregulären Grammatik gibt es nur einen endlichen Automaten mit nur einem Endzustand und umgekehrt. Dies gilt auch für rechtsreguläre Grammatiken wegen der Äquivalenz.

Folgende Größen der linksregulären Grammatik und dem Automaten entsprechen einander:

Grammatik		Automat
T	<=>	X
N	<=>	Z\s0
P	<=>	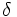$\delta$
S	<=>	se	(Endzustand)

Beim Vergleich von rechtsregulärer Grammatik und Automat ändert sich dabei:

Grammatik		Automat
N	<=>	Z\se
S	<=>	s0	(Anfangszustand)

Für linksreguläre Grammatiken ergibt sich folgende Zuordnung:

A --> Ba	<=>
A --> a	<=>
S --> Ba	<=>
(A --> Aa	<=>	)

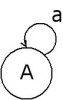Für rechtsreguläre Grammatiken ändert sich dabei:

B --> aA	<=>
A --> a	<=>
B --> aS	<=>
(A --> aA	<=>	)

Einfaches Beispiel:

Rechtsreguläre Grammatik:
G={N,T,P,S}
N={a,1}
T={S,S₂,S_e}
S=S
P={(S --> aS₂), (S₂ --> a| 1 | aS₂ | 1S₂ | ε )}
Es entsteht ein ε-NEA:

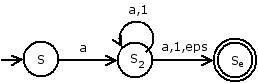
Es zeigt sich, dass diese Grammtik nicht ideal ist, da ein ε-NEA entsteht.

Ändert man P zu P= {(S --> a | S_ea | S_e1)} erhält man eine linksreguläre Grammatik, die das gleiche Problem löst und zugleich ideal ist.