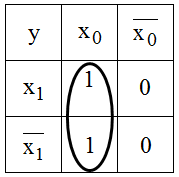Minimierung nach Karnaugh-Veitch

KV-Diagramme eignen sich zur Minimierung von Schaltfunktionen in disjunktiver Normalform (DNF) mit bis zu 5 Variablen (danach werden sie sehr unübersichtlich). Sie stellen nichts anderes als eine andere Anordnung der Wahrheitstafel dar. Der Grundgedanke des auf KV-Diagrammen aufsetzenden Minimierungsverfahrens beruht auf der identischen Umformung und der Darstellung von Mengen.

Aufbau und Ausfüllen eines KV-Diagramms

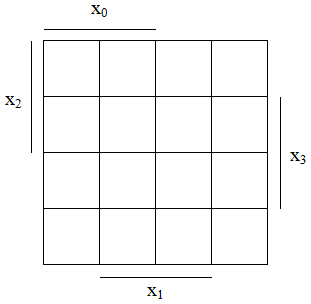
Ein KV-Diagramm für n Eingangsvariablen hat 2ⁿ Felder (siehe Beispiel). Das KV-Diagramm wird mit den Variablen an den Rändern beschriftet. Dabei kommt jede Variable in negierter und nicht-negierter Form vor. Die Zuordnung der Variablen zu den einzelnen Feldern kann dabei beliebig erfolgen, jedoch ist zu beachten, dass sich horizontal und vertikal benachbarte Felder nur in genau einer Variablen unterscheiden dürfen, daher empfiehlt es sich, eine gewisse Struktur einzuhalten.

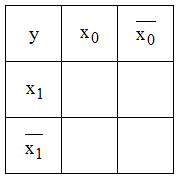
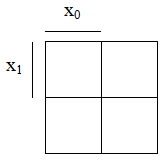
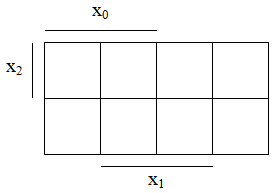
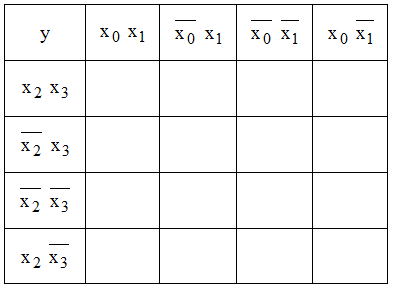
Beispiele für KV-Diagramme mit 2, 3 oder 4 Variablen:

Darstellungen nach Karnaugh	Darstellungen nach Veitch (Menge unter dem Balken hat den Wert "1")

In einem so aufgestellten KV-Diagramm können benachbarte Felder mit gleichen Werten zu Mengen zusammengefasst werden. Mit den bekannten Verknüpfungen Disjunktion, Konjunktion und Komplementation werden diese Mengen dann zu einer vereinfachten Schaltfunktion zusammengefasst.

Beispiel

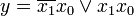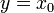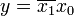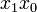Die boolesche Funktion $y = \overline {x_1} x_0 \lor x_1x_0$ kann mit Hilfe der Booleschen Algebra zu $y = x_0$ vereinfacht werden. Im KV-Diagramm werden in den Feldern für $y = \overline {x_1} x_0$ und $x_1x_0$ eine "1" eingetragen, inallen anderen ein "0". Dann versucht man möglichst große Bereiche mit gleichen Zahlen zu Blöcken zusammenzufassen.

Don’t-Care-Zustände

Häufig gibt es Boolesche Funktionen mit Wahrheitstabellen, in denen nicht für jede Kombination der Eingangsvariablen ein Wert der Ausgangsvariablen definiert sein muss. Man nennt solche Ausgangszustände Don’t-Care-Terme und bezeichnet sie mit "x", "-" oder "d", da sie sowohl den Wert 1 als auch 0 annehmen können. Diese Felder dürfen als 1 oder 0 angesehen werden, um in der Minterm- oder Maxterm-Methode Blöcke von Einsen oder Nullen zu vervollständigen.

Vereinfachungen

Um die gegebene Schaltfunktion zu vereinfachen, gibt es nun zwei Möglichkeiten. Sind weniger Felder des KV-Diagramms mit 0 als mit 1 ausgefüllt, wählt man die Minterm-Methode, andernfalls die Maxterm-Methode.

Minterm-Methode

Man versucht, möglichst viele horizontal und vertikal benachbarte Felder, die eine 1 enthalten (Minterme) zu zusammenhängenden 2er-, 4er-, 8er- oder 16er-Blöcken (sogenannten Päckchen) zusammenzufassen. Je nach Wertetabelle kann es jedoch vorkommen, dass es im KV-Diagramm eine allein stehende 1 gibt. Diese allein stehende 1 muss natürlich bei dem späteren Bilden der Schaltfunktion auch berücksichtigt werden.

Ein Block kann unter Umständen über die Ränder des Diagramms fortgesetzt werden. Dies erklärt sich folgendermaßen: KV-Diagramme für drei Variablen müssen im Grunde als Zylinder verstanden werden. Die Felder ganz links und ganz rechts sind also benachbart. KV-Diagramme für vier Variablen müssen im Grunde als Torus („Donut-Form“) verstanden werden. Die vier Ecken des quadratisch gezeichneten KV-Diagrammes sind im Grunde benachbart.

Noch komplexere Nachbarschaftsbeziehungen gelten für 5 oder mehr Variablen. Da multidimensionale Gebilde zeichnerisch schwierig zu handhaben sind, wählt man die Darstellung in der Ebene, muss dann aber die Nachbarschaftsbeziehungen im Sinn behalten. Daher ist es auch sinnvoll KV-Diagramm nur für Schaltprobleme mit wenigen Variablen einzusetzen.

Die gebildeten Päckchen wandelt man nun in Konjunktionsterme um. Dabei werden Variablen innerhalb eines Blockes, die in negierter und nicht negierter Form auftreten, weggelassen.

Diese UND-Verknüpfungen werden durch ODER-Verknüpfungen zusammengefasst und ergeben eine disjunktive Form.

Maxterm-Methode

Die Maxterm-Methode unterscheidet sich von der Minterm-Methode lediglich in folgenden Punkten:

• Statt Einsen werden Nullen zu Päckchen zusammengefasst.
• Ein Päckchen bildet einen Disjunktionsterm (ODER-Verknüpfungen, statt eines Konjunktionsterms).
• Die Disjunktionsterme werden konjunktiv (mit UND) verknüpft.
• Die Variablen werden zusätzlich einzeln negiert.

Anwendungsbeispiel

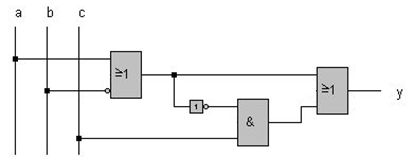
Die Minimierung von Schaltfunktionen nach Karnaugh-Veitch soll nun an einem Beispiel erläutert werden. Ausgangspunkt soll hier das folgende Schaltnetz sein:

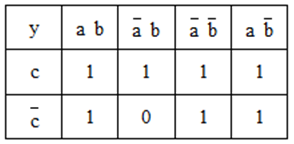
Für dieses Schaltnetz gilt die folgende Schaltwerttabelle, deren Werte in das KV-Diagramm übertragen werden können:

$\begin{array}{c | c | c || c} a & b & c & y \\ \hline 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 \\ \end{array}$

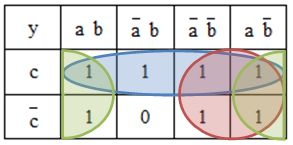
Nun versucht man möglichst große 2er-, 4er- oder 8er-Blöcke zu finden, die nur "1" enthalten, z. B. wie in dieser Möglichkeit:

Möglich wäre in diesem Beispiel auch aus dem grünen 4er-Block einen 2er-Block zu machen, da zwei Felder schon abgedeckt wurden. Allerdings gilt: Je größer die jeweiligen Blöcke sind, desto einfacher wird die Schaltfunktion ausfallen.

Aus den gefundenen Blöcken lassen sich nun Minterme ableiten ...

$\text {blauer Block:} \qquad y_1 = c$
$\text {roter Block:} \qquad y_2 = \overline {b}$
$\text {gruener Block:} \qquad y_3 = a$

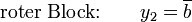
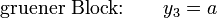
... und disjunktiv zusammenfügen: $y = a \lor \overline {b} \lor c$

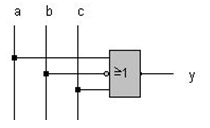
Es zeigt sich also, dass die vorgegebene Originalfunktion durch ein einziges ODER-Gatter ersetzt werden kann, ohne dass das logische Verhalten sich ändert:

In der vorgestellten Lösung gehen wir den Weg über die Bildung der Minterme. Da in diesem Beispiel jedoch wesentlich weniger der Wert "0" als der Wert "1" auftritt, dürfte es einfacher sein, Maxterme zu bilden.

In diesem Fall gibt es nur einen Block mit einer "0". Im Gegensatz zur Bildung der Minterme werden hier die Variablen disjunktiv verknüpft, damit entsteht der Funktionsterm 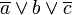$\overline {a} \lor b \lor \overline {c}$. (Würde es nun mehrere solcher Blöcke geben, müssten wir diese konjunktiv zusammenfassen.) Zum Schluss müssen noch alle Variablen einzeln negiert werden, damit erhalten wir schließlich die Schaltfunktion $y = a \lor \overline {b} \lor c$ ... übrigens die gleiche Schaltfunktion, die wir über die Minterme erhalten haben.