Grenzen der Berechenbarkeit
Aus dem präzisierten Algorithmusbegriff lässt sich unmittelbar ein Berechenbarkeitsbegriff ableiten:
| Berechenbarkeitsbegriff |
|
Eine Funktion f mit |
Die Quadratfunktion für natürliche Zahlen ist berechenbar, denn es gibt einen Algorithmus, der für eine eingegebene natürliche Zahl n ihr Quadrat, nämlich n*n berechnet.
Dass es tatsächlich algorithmisch unlösbare Probleme gibt, wollen wir uns am Beispiel von Funktionen zwischen natürlichen Zahlen klar machen. Wir werden sehen, dass es mehr solche Funktionen gibt als Turingmaschinen. Es kann daher nicht jede dieser Funktionen durch eine Turingmaschine, also algorithmisch, berechnet werden.
Was bedeutet nun aber dieses mehr? Es gibt schließlich unendlich viele Turingmaschinen und unendlich viele Funktionen von den natürlichen Zahlen in die natürlichen Zahlen. Aber es gibt Unterschiede im Unendlichen. Man unterscheidet zwischen abzählbar und überabzählbar unendlichen Mengen.
| Jede unendliche Menge, deren Elemente sich umkehrbar eindeutig (bijektiv, eineindeutig) den natürlichen Zahlen zuordnen lässt, heißt abzählbar, andernfalls heißt sie überabzählbar. |
Beispielsweise ist die Menge aller Worte über einem endlichen Alphabet abzählbar. Dies begründen wir für das Alphabet {a, b, c, ..., z}. Die Worte der Länge 1 entsprechen den natürlichen Zahlen von 1 bis 26:
a b c ... x y z | | | | | | 1 2 3 ... 24 25 26
Es gibt 262 Worte der Länge 2. Sie entsprechen den natürlichen Zahlen von 26 + 1 bis 26 + 262:
aa ab ac az ba bz za zz | | | | | | | | 26+1 26+2 26+3 ... 2*26 2*26+1 ... 3*26 ... 262+1 ... 262+26
Es gibt 26n Worte der Länge n (n > 1). Sie entsprechen den natürlichen Zahlen von r + 1 bis r + 26n, wobei r = 26 + 262 + ... + 26n-1:
aaa...a aaa...b aaa...c ... zzz...z | | | | r+1 r+2 r+3 r+26n
Man kann jedes beliebige Wort endlicher Länge irgendwo in dieser Liste finden, zu ihm gehört eine eindeutig bestimmte Nummer. Die Worte lassen sich also mit den natürlichen Zahlen paaren.
Da jede Turingmaschine sich durch eine endliche Zeichenkette angeben lässt, nämlich durch ihre Turingtafel, kann man auch alle Turingmaschinen umkehrbar eindeutig den natürlichen Zahlen zuordnen. Man kann also alle Turingmaschinen durchnummerieren:
T1, T2, T3, ...
Die Menge aller Turingmaschinen ist also abzählbar unendlich.
Dagegen ist die Menge aller Funktionen von den natürlichen Zahlen in die natürlichen Zahlen überabzählbar. Diese Menge enthält zu viele Funktionen, als dass sie mit den natürlichen Zahlen gepaart werden könnten. Dies beweisen wir indirekt. Wir nehmen an, die Menge wäre abzählbar, die Funktionen könnten als durchnummeriert werden, etwa
f1, f2, f3, ...
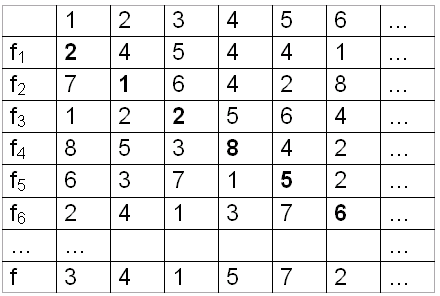
Die Funktionswerte einer beliebigen Funktion in dieser Aufzählung stellen eine Folge natürlicher Zahlen dar. Notieren wir die Folgenglieder nebeneinander und alle Funktionen untereinander, so erhalten wir ein doppelt unendliches Schema natürlicher Zahlen, z. B.:
Wir können dann eine neue Funktion f definieren, indem wir den ersten Funktionswert der ersten Funktion, den zweiten Funktionswert der zweiten Funktion, allgemein fn(n), abändern und den geänderten Wert für f(n) wählen. In unserem Beispiel haben wir etwa f(1) = 3 statt f1(1) = 2 und f(2) = 4 statt f2(2) = 1 gewählt. Die Funktion f stimmt dann mit keiner der Funktionen aus der Liste überein, denn es ist 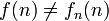 für alle
für alle 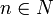 . Damit ist die Annahme, dass wir in dieser Liste alle Funktionen erfasst haben, zum Widerspruch geführt.
. Damit ist die Annahme, dass wir in dieser Liste alle Funktionen erfasst haben, zum Widerspruch geführt.
Die Menge der Funktionen von den natürlichen Zahlen in die natürlichen Zahlen ist also überabzählbar unendlich. Es gibt demnach solche Funktionen, die nicht von einer Turingmaschine berechenbar sind. Dabei sagen wir, eine Turingmaschine berechnet eine Funktion F, wenn sie zur Bandinschrift n in unärer Darstellung den Funktionswert F(n) in unärer Darstellung ausgibt.
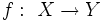 , wobei
, wobei 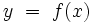 , für
, für 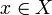 und
und 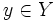 , falls f(x) existiert, ist berechenbar, wenn es einen Algorithmus gibt, der die Abbildung realisiert bzw. wenn es eine Turingmaschine gibt, die diese Funktion realisiert.
, falls f(x) existiert, ist berechenbar, wenn es einen Algorithmus gibt, der die Abbildung realisiert bzw. wenn es eine Turingmaschine gibt, die diese Funktion realisiert.